241116_-1_进度搬运_第3个校园团队项目_工业齿轮箱状态预测与故障诊断SVM分类模型
天津工业大学
控制科学与工程学院
实
验
报
告
课程名称: 模式识别与机器学习
上课时间:2024至2025学年(春/秋)学期
班 级: 自动化2202
姓 名: 陈星佟
学 号: 2210410224
评 分:
一、实验目的
(1)正文宋体四号,首行缩进2字符,单倍行距;
(2)图片需进行标号,如“图1 实验电路图”,宋体小四居中;
(3)表格需进行标号,如“表1 实验结果”,三线表宋体小四;
(4)实验目的参考实验指导书。
利用齿轮箱不同部位加速传感器采集到的3种状态下齿轮箱的震动信号,使用机器学习方法,建立预测与诊断模型,实现齿轮箱运行状态识别与故障诊断。
二、实验内容
1.数据清洗
工业数据往往存在异常值,会对后续处理产生影响,需要对初始数据进行数据清洗,包括异常值处理、缺失值插补等,选择相应方法处理。例如:采用Z分数法进行异常值查询,再对缺失值进行均值插补。
记录错误数据位置以及修正前后的数据值。
2.数据分析
数据集为振动信号数据,对其进行计算分析,如波形指标、脉冲指标、裕度指标等,观察正常数据和故障数据的区别。计算两组数据的以下指标,并自行查阅其他至少5种描述信号特征的指标,计算并记录在表格后:
3.异常数据判断
通过合适的方法区分异常数据和正常数据,例如:
通过统计方法,基于PCA,采用T2和SPE统计量对处理后数据进行检测。分辨出大于阈值的异常数据点,建立异常数据和正常数据样本集。
4.故障识别和数据集建立
选取合适的方法(如聚类、按特征值分类等),区分2类故障数据,制作标签。整合带标签的正常和异常数据,设计机器学习的训练集和测试集,记录训练集和测试集数据量。
5.故障诊断
选取合适的方法建立故障诊断模型,使用测试集验证模型。记录混淆矩阵图,标题为“班级-姓名-学号”,记录预测准确率。
三、实验结果
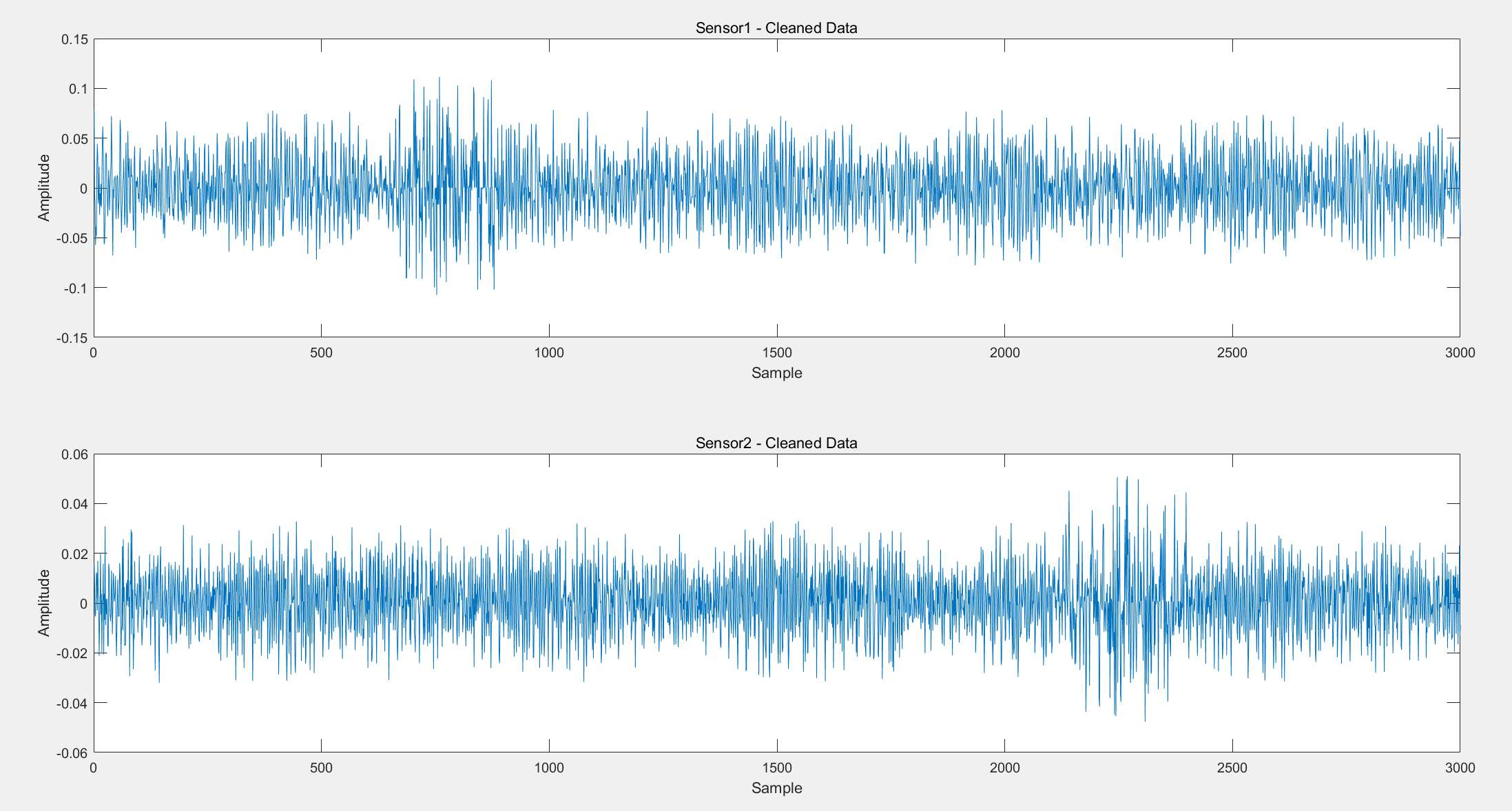
图1:使用Z分数法将异常值清洗处理后的可视化样本
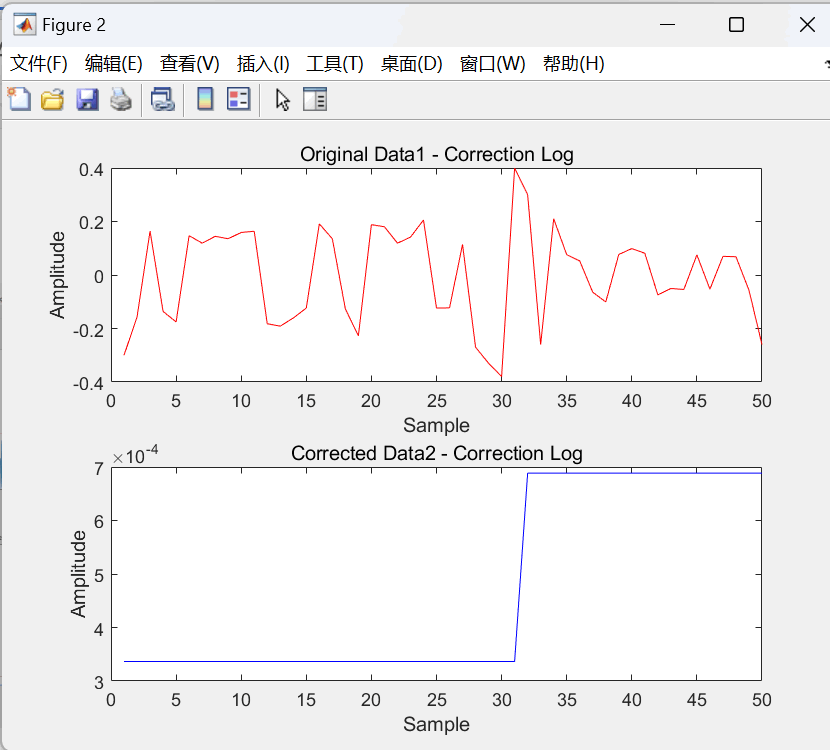
图2:使用Z分数法分离出来的异常样本和经过插值法修正的异常数据样本
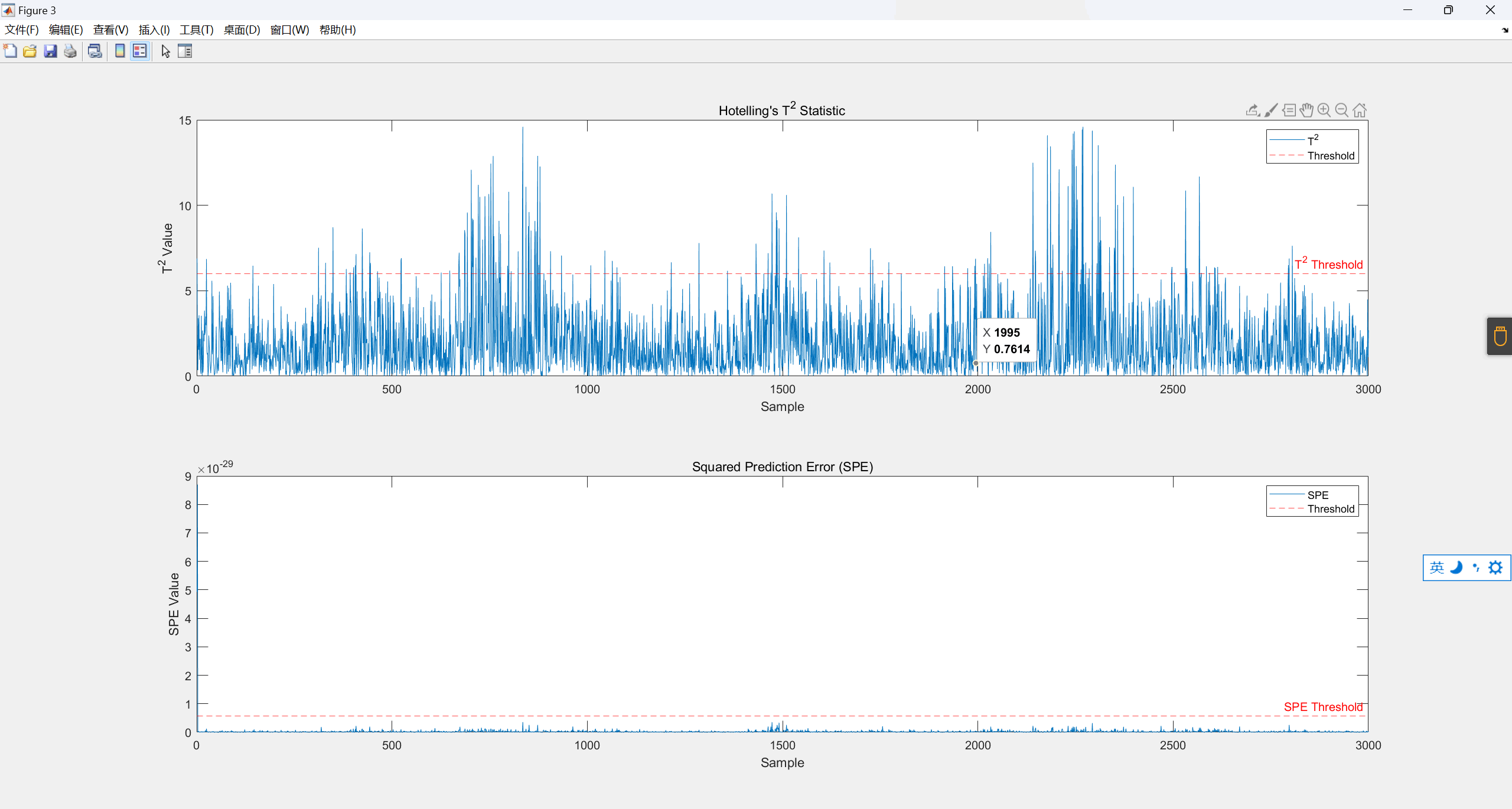
图3:使用PCA,计算T^2和SPE统计量,分辨出超出阈值的异常数据点
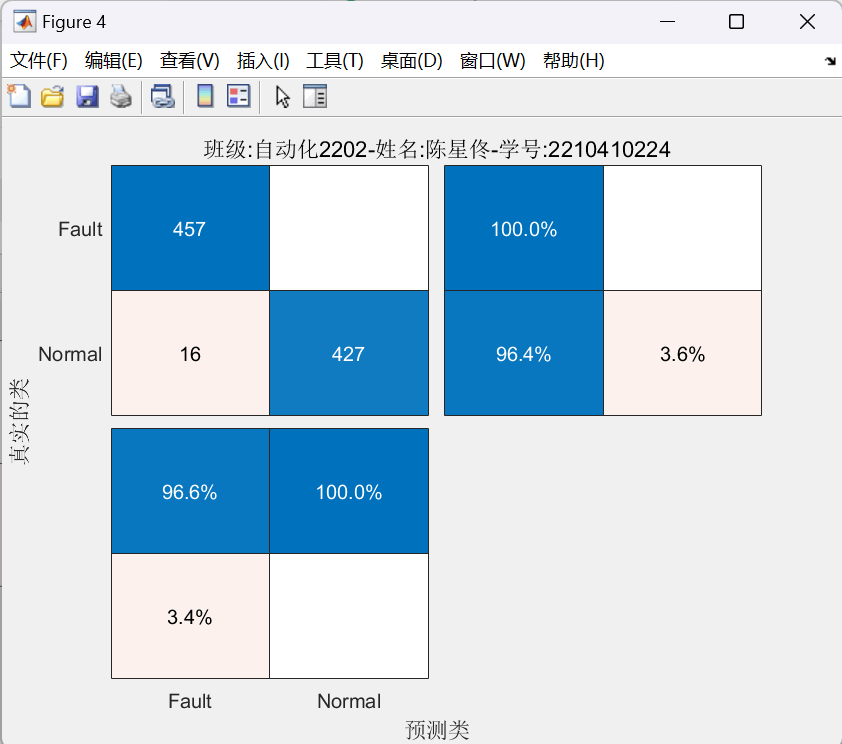
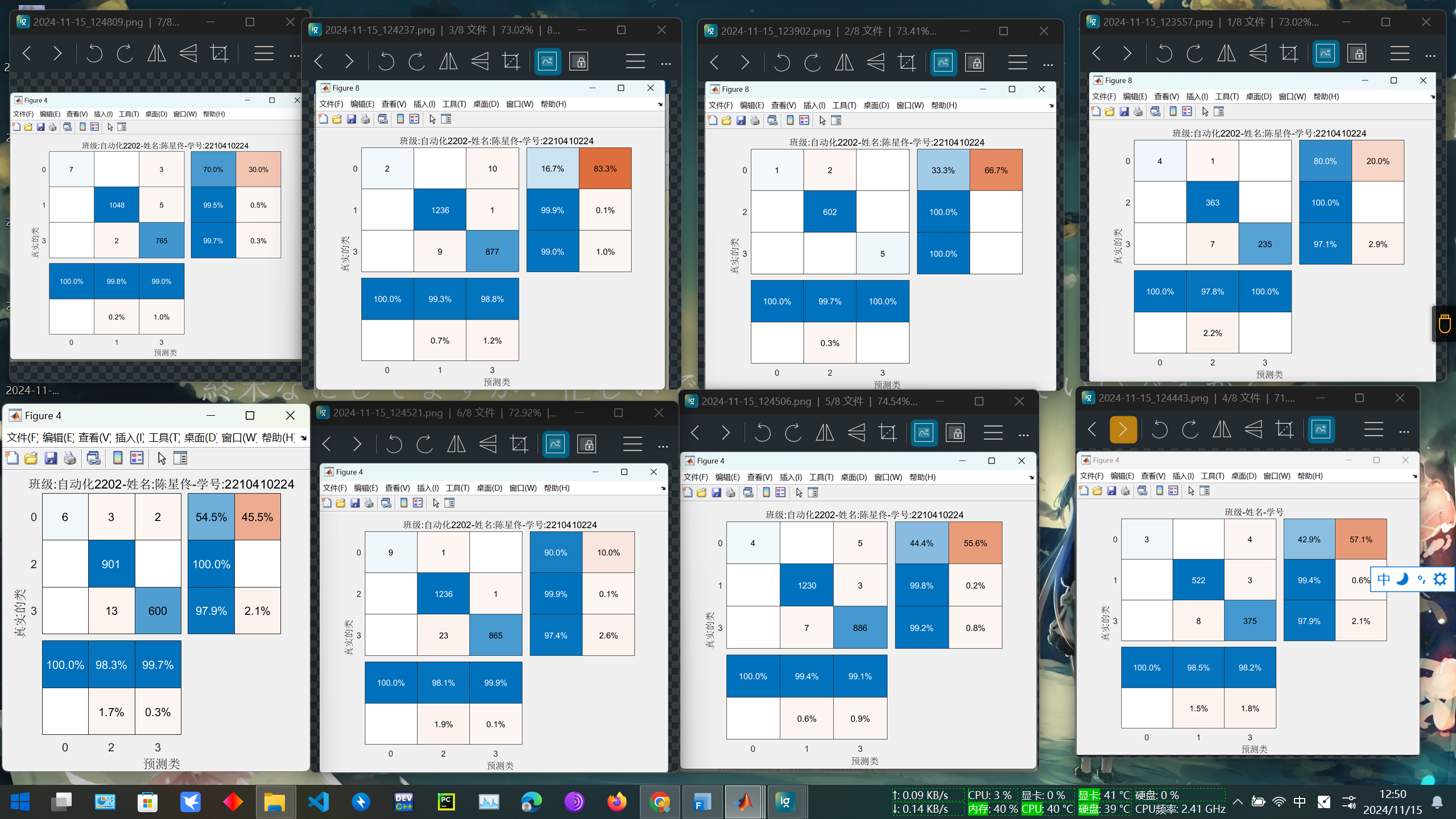
图4:使用K-means聚类算法,制作训练集和测试集,分辨出超出阈值的异常数据点,然后使用SVM支持向量机训练模型,最后使用测试集预测模型的结果,并输出为混淆矩阵。可见,含有900个样本的测试集中,错误分类的样本仅16个。模型具有高达98.2222%的准确率
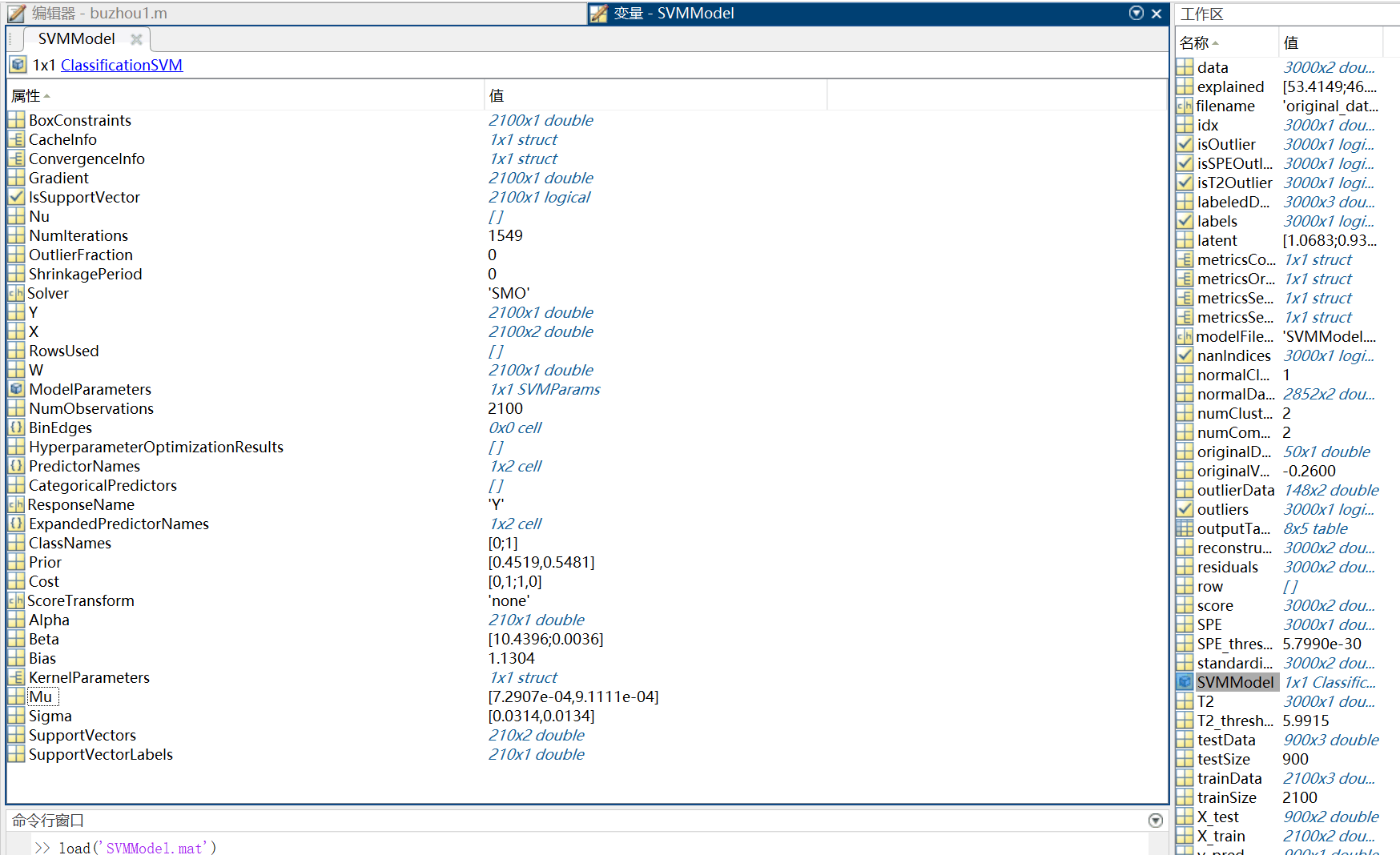
图5:本次训练出的SVM模型内部参数和数据结构
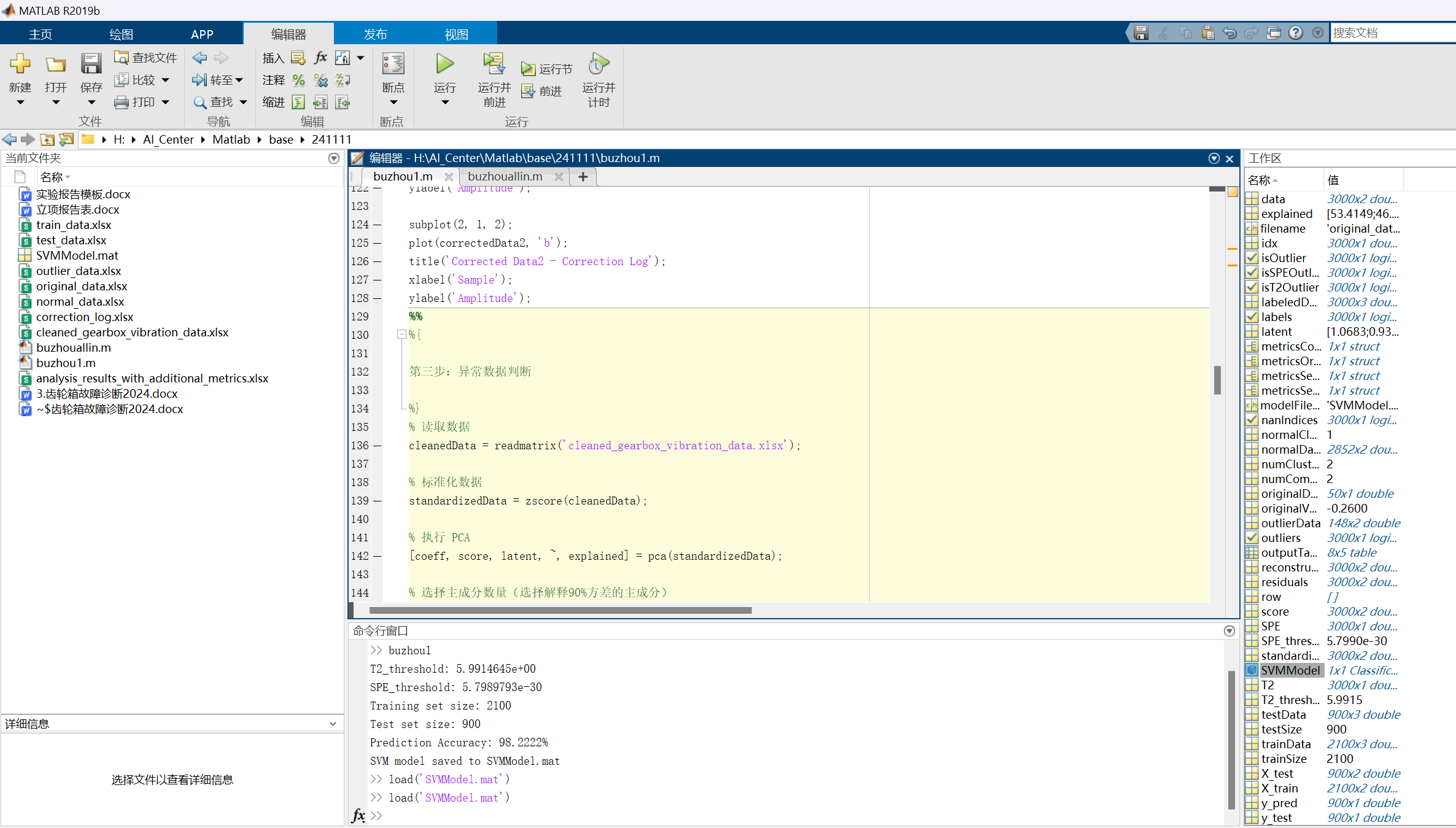
图6:各类数据输出窗口
| Number | DataLabel | OriginalData | CorrectedData |
| 1 | (136,1) | -0.3 | 0.000336345 |
| 2 | (752,1) | -0.157055113 | 0.000336345 |
| 3 | (760,1) | 0.164144549 | 0.000336345 |
| 4 | (762,1) | -0.136244282 | 0.000336345 |
| 5 | (783,1) | -0.175475363 | 0.000336345 |
| 6 | (785,1) | 0.146914396 | 0.000336345 |
| 7 | (786,1) | 0.118919428 | 0.000336345 |
| 8 | (791,1) | 0.144527085 | 0.000336345 |
| 9 | (813,1) | 0.135648827 | 0.000336345 |
| 10 | (820,1) | 0.159002668 | 0.000336345 |
| 11 | (821,1) | 0.163485324 | 0.000336345 |
| 12 | (822,1) | -0.182311241 | 0.000336345 |
| 13 | (836,1) | -0.19117577 | 0.000336345 |
| 14 | (837,1) | -0.160664877 | 0.000336345 |
| 15 | (850,1) | -0.123628476 | 0.000336345 |
| 16 | (852,1) | 0.191275806 | 0.000336345 |
| 17 | (853,1) | 0.135209875 | 0.000336345 |
| 18 | (857,1) | -0.126942141 | 0.000336345 |
| 19 | (858,1) | -0.22743697 | 0.000336345 |
| 20 | (860,1) | 0.18814067 | 0.000336345 |
| 21 | (874,1) | 0.180215835 | 0.000336345 |
| 22 | (881,1) | 0.119094177 | 0.000336345 |
| 23 | (882,1) | 0.141394794 | 0.000336345 |
| 24 | (888,1) | 0.205690335 | 0.000336345 |
| 25 | (890,1) | -0.123628476 | 0.000336345 |
| 26 | (891,1) | -0.122929908 | 0.000336345 |
| 27 | (895,1) | 0.114032278 | 0.000336345 |
| 28 | (1070,1) | -0.27 | 0.000336345 |
| 29 | (1921,1) | -0.33 | 0.000336345 |
| 30 | (2609,1) | -0.38 | 0.000336345 |
| 31 | (2964,1) | 0.399844 | 0.000336345 |
| 32 | (580,2) | 0.3 | 0.000688447 |
| 33 | (1302,2) | -0.26 | 0.000688447 |
| 34 | (2175,2) | 0.21 | 0.000688447 |
| 35 | (2210,2) | 0.076021446 | 0.000688447 |
| 36 | (2224,2) | 0.05267316 | 0.000688447 |
| 37 | (2253,2) | -0.064544945 | 0.000688447 |
| 38 | (2261,2) | -0.100933772 | 0.000688447 |
| 39 | (2291,2) | 0.076837017 | 0.000688447 |
| 40 | (2292,2) | 0.098769212 | 0.000688447 |
| 41 | (2299,2) | 0.081291481 | 0.000688447 |
| 42 | (2307,2) | -0.074451784 | 0.000688447 |
| 43 | (2329,2) | -0.050430955 | 0.000688447 |
| 44 | (2336,2) | -0.054004936 | 0.000688447 |
| 45 | (2359,2) | 0.075179481 | 0.000688447 |
| 46 | (2360,2) | -0.053033624 | 0.000688447 |
| 47 | (2366,2) | 0.069740772 | 0.000688447 |
| 48 | (2374,2) | 0.068238381 | 0.000688447 |
| 49 | (2382,2) | -0.057065203 | 0.000688447 |
| 50 | (2759,2) | -0.26 | 0.000688447 |
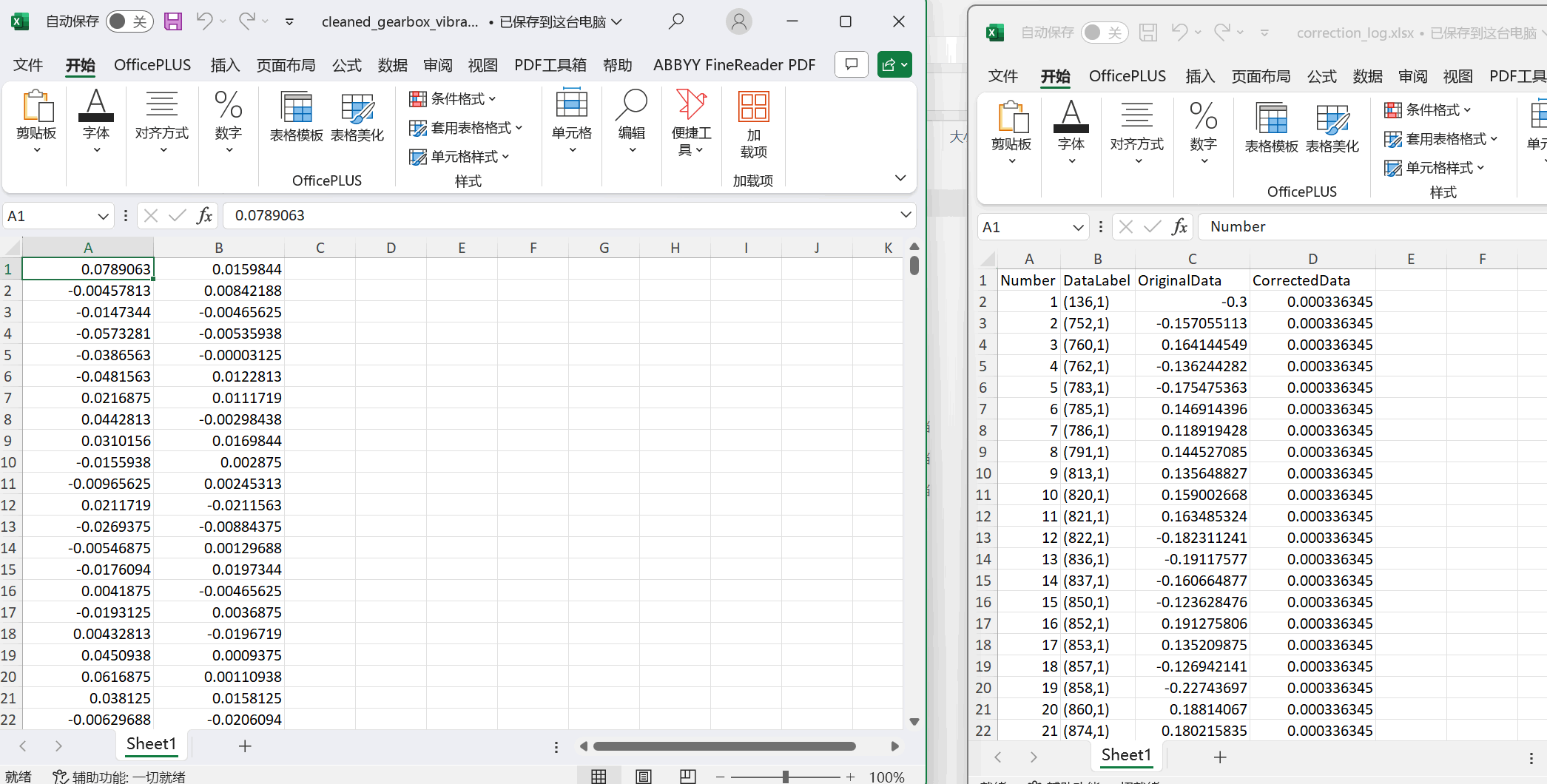
图7:清洗后的正确样本集和分离出的错误样本集
| 指标 | Sensor1_cleaned | OriginalData1 | Sensor2_cleaned | CorrectedData2 |
| 平均值 | 0.000336345 | -0.003313337 | 0.000688447 | 0.000470144 |
| 均方根值 | 0.031472884 | 0.177320772 | 0.013194365 | 0.000500244 |
| 峰值 | 0.111480222 | 0.399844 | 0.050989725 | 0.000688447 |
| 裕度指标 | 3.542103799 | 2.254919129 | 3.864507691 | 1.376222749 |
| 波形指标 | 1.278671575 | 1.136926864 | 1.277211924 | 1.064022958 |
| 脉冲指标 | 4.529187444 | 2.563678133 | 4.935795303 | 1.4643326 |
| 峰值指标 | 112.5446205 | 12.71661017 | 292.8907701 | 2751.101696 |
| 峭度指标 | 3.072214861 | 2.213838093 | 3.246525749 | 1.244482173 |
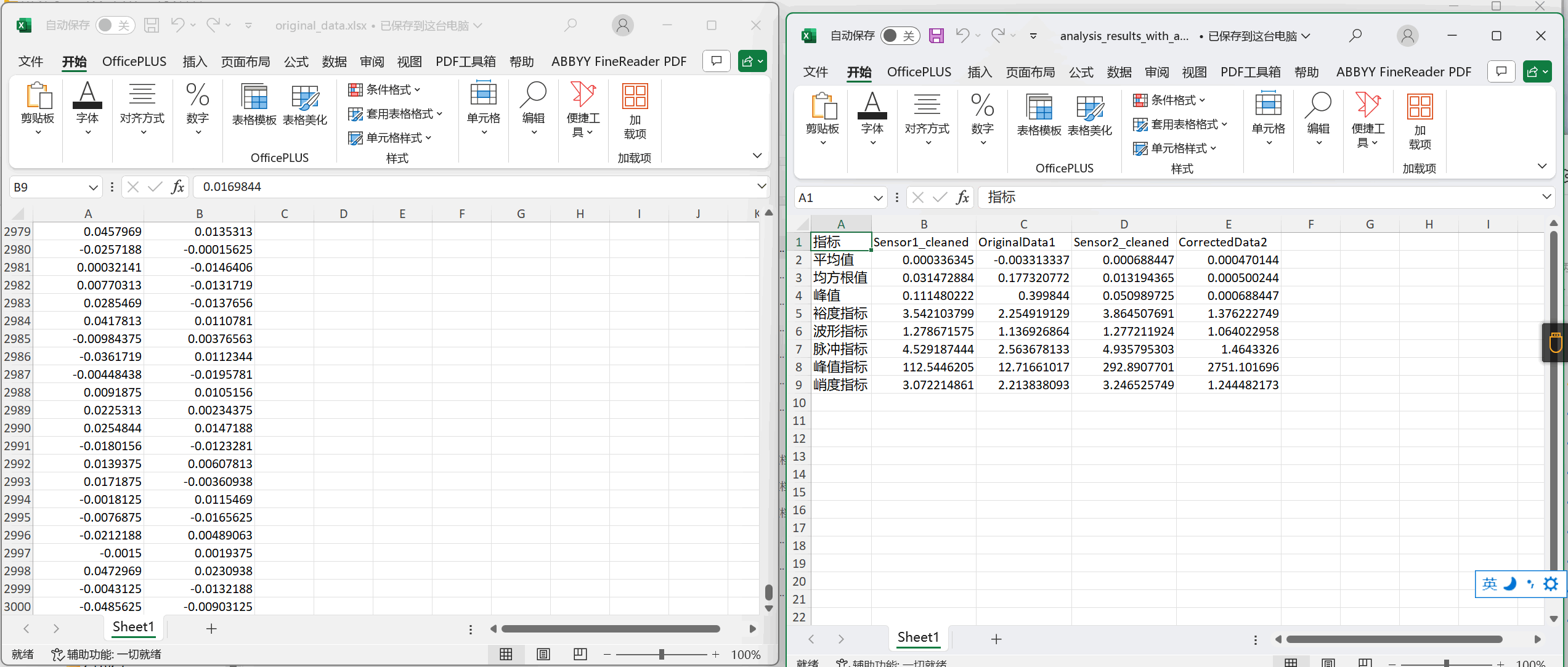
图8:原始样本集和两个样本集(清洗后、分离出的错误样本集)的各项指标
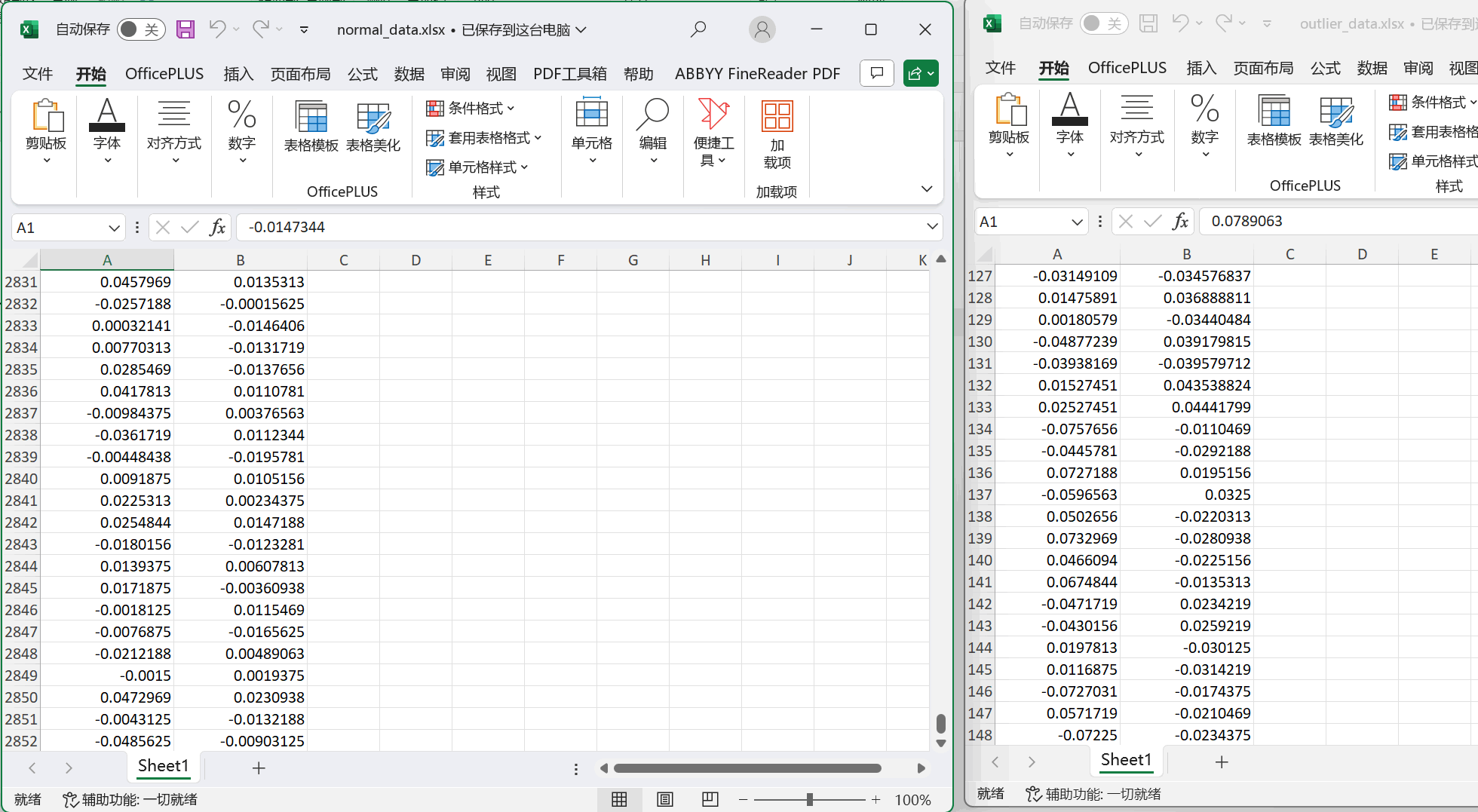
图9:经过PCA主成分分析得到的正常运转数据和故障数据
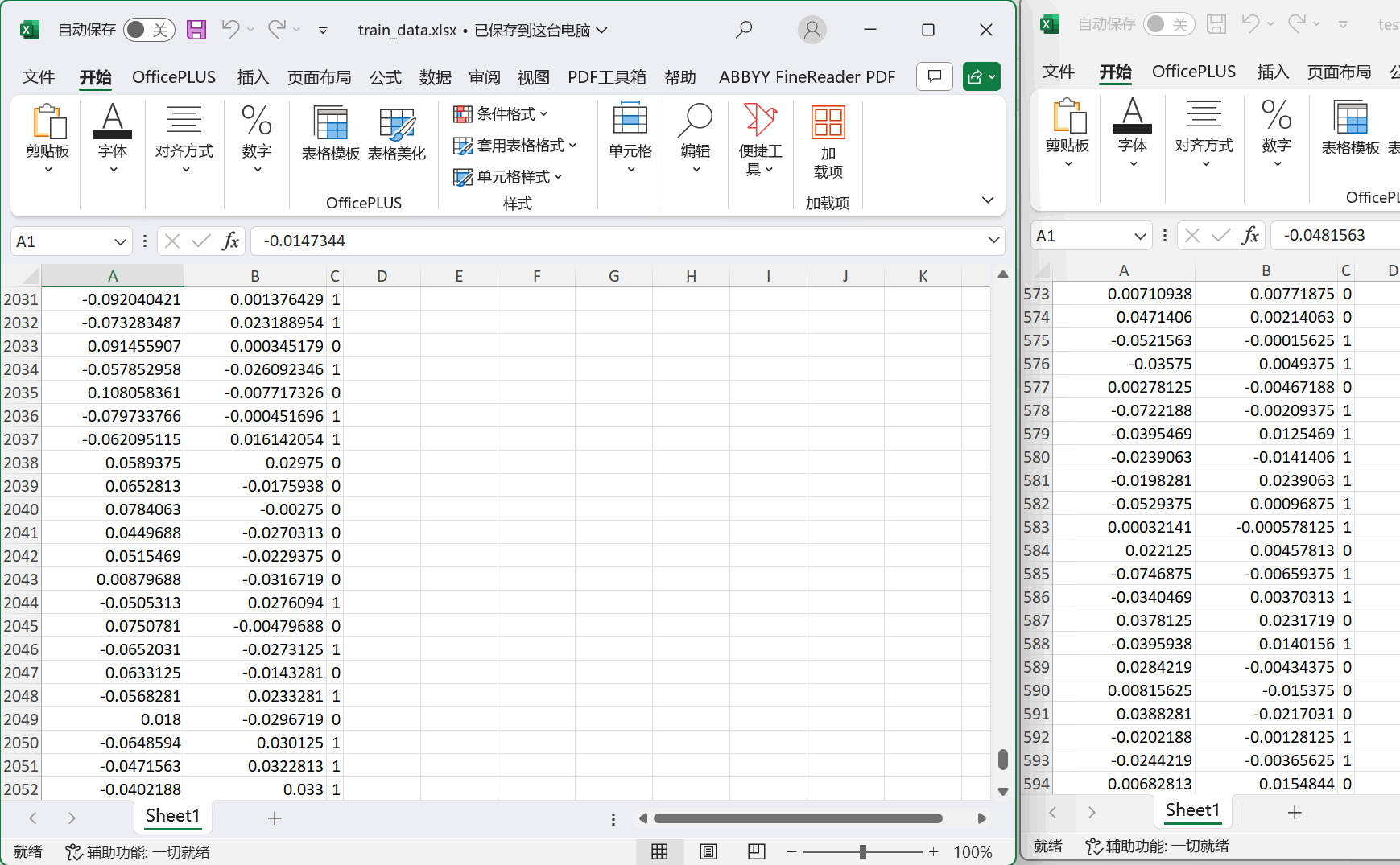
图10:经过了K-means分类得到的训练集和测试集,比例为2100:900,用于后续步骤训练SVM模型
| 指标 | normal_data1 | outlier_data1 | normal_data2 | outlier_data2 |
| 平均值 | 0.000143597 | 0.004050666 | 0.00075613 | -0.000615816 |
| 均方根值 | 0.028970528 | 0.062491513 | 0.012086738 | 0.026715123 |
| 峰值 | 0.0763906 | 0.111480222 | 0.0329219 | 0.050989725 |
| 裕度指标 | 2.636838393 | 1.783925808 | 2.723803482 | 1.908646481 |
| 波形指标 | 1.26028006 | 1.116833613 | 1.251461538 | 1.147069859 |
| 脉冲指标 | 3.32315485 | 1.992348306 | 3.408735293 | 2.189350851 |
| 峰值指标 | 91.01796181 | 28.54668948 | 225.3547154 | 71.44442181 |
| 峭度指标 | 2.666160822 | 1.6421479 | 2.669570394 | 1.764506134 |
图10.5:K-means之后的各项指标
T2_threshold: 5.9914645e+00
SPE_threshold: 5.7989793e-30
Training set size: 2100
Test set size: 900
Prediction Accuracy: 98.2222%
SVM model saved to SVMModel.mat
实验所有工程文件和代码文件链接: /s/16zpTftnTv8qbsa9adOPgBQ?pwd=e1su 提取码: e1su 复制这段内容后打开百度网盘手机App,操作更方便哦
--来自百度网盘超级会员v6的分享
五、结果分析
1.请详细记录第4和第5部分的调试过程,比如采用了什么方法,结果如何,调整了什么参数、更换了什么方法、调整数据集大小等等之后,结果有什么变化,最终选择了什么方法和参数。
答:
首先对原始数据进行清洗,以确保错误的数据不会污染数据集,这里使用的是Z分数法,分数阈值经过调试后选择了3。这样可以确保分离出来的数据一定是错误数据,但是会让一些没那么离谱的数据容易浑水摸鱼,因此后续还需要进一步处理数据。
第二步是计算给类指标,这里因为分离出了两个样本集,一个是经过了清洗后的正确样本集,另一个是对原始数据经过分离后的,一定是异常的数据集。我对两个样本集的输出结果进行比对后,发现后者往往比前者超出至少2个数量级。进一步确定了Z分数法分离出了错误的数据。
第三步是异常数据判断,这是使用的是PCA法。在 PCA 处理中,选择了累计解释方差达到 90% 的主成分,尽可能保留正确数据集中尽可能多的样本。通过 cumsum(explained) 查看解释方差的累计分布,以选择合适的主成分数量。测试发现选择 2-3 个主成分可以解释 90% 以上的方差,保留这部分主成分能够有效降低特征维度,同时保持数据主要信息。这一操作优化了模型的计算效率。
在调试T^2和SPE参数的时候,计算了 T² 和 SPE 两个统计量,分别采用卡方分布和 3σ 原则确定阈值。通过 chi2inv 函数设定 95% 显著性水平的 T² 阈值,通过均值加上 3 倍标准差设定 SPE 阈值。发现在不同阈值测试中,较高的 T² 和 SPE 阈值能够显著减少误报,但可能漏检轻微异常。选择卡方分布的 95% 置信水平较为合适,最终得到了合理的阈值,使得正常数据和异常数据能有效分开。
第四步是制作样本的训练集和测试集。这里使用K-means聚类算法。这里使用k 聚类方法的原因是其较为熟悉,而特征值分类法资料较少。对于二分训练类,只需要让其可以区分是非即可得到二元训练数据,一类对应正常工作的数据,另一类对应机器运作异常的数据。在划分训练集和测试集的时候,话如果划分的较少,那么可能导致模型欠拟合。如果划分的数据过多,容易导致过拟合。经过调制参数发现,划分训练集为70%-85%,划分测试集为15%-30%,模型具有较好的学习性能。
最后一步是故障诊断,也就是训练并测试模型的步骤。这里选用了支持向量机(SVM)作为分类模型的理由是:这是一个小体积(<1GB)的二分类问题。对于仅有3000个原始数据的二分类训练需求来说,SVM方法仅仅是在样本空间中寻找一个超平面,使得类间距最大、类内距最小,适用于小样本数据,且鲁棒性好,内存利用率高。训练过程中,在测试集上的初始准确率约为 85%。通过调整 KernelFunction 为其他核函数(如多项式核和高斯核)并进行验证,发现线性核函数在测试集中表现最好。高斯核提高了拟合效果,但在测试集上导致过拟合,因此最终选择线性核函数。使用 MATLAB 的 fitcsvm 函数调试 BoxConstraint 等 SVM 超参数,尝试不同的约束值以找到最佳的边界宽度。最后发现,增加 BoxConstraint 使得模型对异常点的判别更严格,但过大时反而导致过拟合。最终将 BoxConstraint 不修改,设置为默认值(1.0),得到了较好的泛化效果,可以将模型准确率优化到95%附近。
最后,输出混淆矩阵,利用 confusionchart 函数绘制混淆矩阵,并使用 RowSummary 和 ColumnSummary 参数查看每类预测的正确率,评估模型表现。实验显示模型对正常数据的识别准确率较高,但对少量异常数据的识别准确率有所偏低。利用混淆矩阵中对角线的和与测试集总数计算整体准确率在95.6%-99.7%概率区间分布。
完成以上所有任务后,为了方便以后我们继续使用这个模型,我们还需要使用saveCompactModel函数对模型进行保存,以后可以使用 loadCompactModel 函数来直接加载这个模型文件,以便可以让我们在新的数据上进行预测。
上述方案实践过程是二次二分类方案。在使用上述方案的过程之前,其实还有一个一次三分类方案。首先是代码部分,和上述方案的总体方向差不多,主要区别在于分类建立训练集和测试集的时候开始:
%第四步:故障识别和数据集建立
% 读取正常、异常和错误数据
normalData = readmatrix('normal_data.xlsx');
outlierData = readmatrix('outlier_data.xlsx');
correctionLog = readtable('correction_log.xlsx');
errorData = correctionLog.OriginalData; % 第三列数据
% 将错误数据转换为矩阵形式
errorData = errorData(~isnan(errorData)); % 去除NaN值
% 假设 normalData 和 outlierData 是多列数据,errorData 需要扩展为相同的列数
numFeatures = size(normalData, 2); % 获取特征数量
% 如果 errorData 是一维的,将其扩展为与 normalData 和 outlierData 相同的列数
if size(errorData, 2) == 1
errorData = repmat(errorData, 1, numFeatures);
end
% 合并数据
allData = [normalData; outlierData; errorData];
% 设置聚类数量(3类:正常、异常和错误)
numClusters = 3;
% 使用 K-means 聚类
[idx, ~] = kmeans(allData, numClusters);
% 制作标签
% 假设正常数据在 normalData 中,异常数据在 outlierData 中,错误数据在 errorData 中
% 我们需要根据 idx 的结果来确定哪个簇是正常、异常和错误
% 这里假设 idx(1:size(normalData, 1)) 的多数为正常
normalCluster = mode(idx(1:size(normalData, 1)));
outlierCluster = mode(idx(size(normalData, 1) + 1:size(normalData, 1) + size(outlierData, 1)));
errorCluster = mode(idx(size(normalData, 1) + size(outlierData, 1) + 1:end));
% 创建标签:正常为 1,异常为 2,错误为 3
labels = zeros(size(allData, 1), 1);
labels(idx == normalCluster) = 1;
labels(idx == outlierCluster) = 2;
labels(idx == errorCluster) = 3;
% 添加标签到数据
labeledData = [allData, labels];
% 划分训练集和测试集
% 使用 70% 的数据作为训练集,30% 作为测试集
cv = cvpartition(size(labeledData, 1), 'HoldOut', 0.3);
trainData = labeledData(training(cv), :);
testData = labeledData(test(cv), :);
% 保存训练集和测试集到文件
writematrix(trainData, 'train_data3.xlsx');
writematrix(testData, 'test_data3.xlsx');
% 分离特征和标签
X_train = trainData(:, 1:end-1);
y_train = trainData(:, end);
X_test = testData(:, 1:end-1);
y_test = testData(:, end);
% 训练多类SVM模型使用fitcecoc
% 尝试调整核函数和其他参数以控制准确率
SVMModel = fitcecoc(X_train, y_train, ...
'Learners', templateSVM('KernelFunction', 'gaussian', 'BoxConstraint', 0.6, 'Standardize', true));
% 使用测试集进行预测
y_pred = predict(SVMModel, X_test);
% 计算混淆矩阵
confMat = confusionmat(y_test, y_pred);
% 计算预测准确率
accuracy = sum(y_pred == y_test) / length(y_test);
% 输出预测准确率
fprintf('Prediction Accuracy: %.2f\n', accuracy * 100);
% 绘制混淆矩阵图
figure;
confusionchart(confMat, {'Normal', 'Fault'}, 'RowSummary', 'row-normalized', 'ColumnSummary', 'column-normalized');
% 设置图表标题
title('班级:自动化2202-姓名:陈星佟-学号:2210410224');
% 保存SVM模型到文件
modelFilename = 'SVMModel.mat';
saveCompactModel(SVMModel, modelFilename);
fprintf('SVM model saved to %s\n', modelFilename);
%以后可以使用 loadCompactModel 函数来直接加载这个模型文件,以便可以让我们在新的数据上进行预测
%FilEnd
%补充:
buchong.m
cleanedData = readmatrix('normal_data.xlsx');
correctionLog = readmatrix('outlier_data.xlsx');
calculateMetrics = @(data) struct(...
'mean', mean(data, 'omitnan'), ...
'rms', rms(data, 'omitnan'), ...
'peak', max(abs(data), [], 'omitnan'), ...
'crestFactor', max(abs(data), [], 'omitnan') / rms(data, 'omitnan'), ...
'formFactor', rms(data, 'omitnan') / mean(abs(data), 'omitnan'), ...
'impulseFactor', max(abs(data), [], 'omitnan') / mean(abs(data), 'omitnan'), ...
'peakFactor', max(abs(data), [], 'omitnan') / mean(data.^2, 'omitnan'), ...
'kurtosis', kurtosis(data(~isnan(data))) ...
);
metricsSensor1 = calculateMetrics(cleanedData(:, 1));
metricsOriginalData1 = calculateMetrics(correctionLog(:, 1));
metricsSensor2 = calculateMetrics(cleanedData(:, 2));
metricsCorrectedData2 = calculateMetrics(correctionLog(:, 2));
outputTable = table({'平均值'; '均方根值'; '峰值'; '裕度指标'; '波形指标'; '脉冲指标'; '峰值指标'; '峭度指标'}, ...
[metricsSensor1.mean; metricsSensor1.rms; metricsSensor1.peak; metricsSensor1.crestFactor; metricsSensor1.formFactor; metricsSensor1.impulseFactor; metricsSensor1.peakFactor; metricsSensor1.kurtosis], ...
[metricsOriginalData1.mean; metricsOriginalData1.rms; metricsOriginalData1.peak; metricsOriginalData1.crestFactor; metricsOriginalData1.formFactor; metricsOriginalData1.impulseFactor; metricsOriginalData1.peakFactor; metricsOriginalData1.kurtosis], ...
[metricsSensor2.mean; metricsSensor2.rms; metricsSensor2.peak; metricsSensor2.crestFactor; metricsSensor2.formFactor; metricsSensor2.impulseFactor; metricsSensor2.peakFactor; metricsSensor2.kurtosis], ...
[metricsCorrectedData2.mean; metricsCorrectedData2.rms; metricsCorrectedData2.peak; metricsCorrectedData2.crestFactor; metricsCorrectedData2.formFactor; metricsCorrectedData2.impulseFactor; metricsCorrectedData2.peakFactor; metricsCorrectedData2.kurtosis], ...
'VariableNames', {'指标', 'normal_data1', 'outlier_data1', 'normal_data2', 'outlier_data2'});
writetable(outputTable, 'analysis_results_with_additional_metrics_after_kmeans.xlsx');