240210_-1_进度搬运_第1个校园团队项目_基于Hopfield神经网络的外卖起手派送路径优化方案

05publishedweb/W002-学习进度/DocxerAttachments/QQ浏览器截图20190926182728 1.png

实 验 报 告

课程名称： 智能控制技术

实验名称：基于Hopfield神经网络的路径优化

实验地点： 控制学院c209

专业班级： 自动化2202

学生姓名： 陈星佟

学 号： 2210410224

任课教师： 王琨

开课时间：2024 - 2025年（秋）学期

开课学院：控制科学与工程学院

实验三 基于Hopfield神经网络的路径优化

一、实验目标

  1. 理解Hopfield神经网络的工作原理；

  2. 掌握Hopfield神经网络的编程方法；

  3. 能够根据问题的复杂性设计合理的Hopfield神经网络结构。

二、实验内容

旅行商路径优化问题(Traveling Salesman Problem，简称TSP)：已知N个城市之间的相互距离，现有一推销员(旅行商)必须遍访这N个城市，并且每个城市只能访问一次，最后又必须返回出发城市。设计Hopfield神经网络安排他对这些城市的访问次序，使其旅行路线的总长度最短。完成神经网络的设计和仿真。

三、实验步骤

  1. TSP问题是在一个城市集合中找出一个最短且经过每个城市各一次并回到起点的路径。为了将TSP问题映射为一个神经网络的动态过程，Hopfield采取了换位矩阵的表示方法，用N×N矩阵表示商人访问N个城市。例如，有四个城市 ，访问路线是： ，则Hopfield网络输出所代表的有效解用下面的二维矩阵表1来表示：

表1：4个城市的访问路线

表1：4个城市的访问路线

表1构成了一个4×4的矩阵，该矩阵中，各行各列只有一个元素为1，其余为0，否则是一个无效的路径。采用 表示神经元 的输出，相应的输入用 表示。如果城市 在 位置上被访问，则 ，否则 。

  1. 针对TSP问题，定义如下形式的能量函数：

(1)

式中，A和D是权值， 表示城市x到城市 y之间的距离。

Hopfield网络的动态方程为：

(2)

  1. 采用Hopfield网络求解TSP问题的算法描述如下：

（1） 置初值：t=0，A=1.5，D=1.0，μ=50；

（2） 计算N个城市之间的距离 ；

（3） 神经网络输入 的初始化在0附近产生；

（4） 利用动态方程(2)计算 ；

（5） 根据一阶欧拉法离散化式(2),求

（6）为了保证收敛于正确解，即矩阵V各行各列只有一个元素为1，其余为0，采用Sigmoid函数计算

其中μ>0，μ值的大小决定了Sigmoid函数的形状。

(7) 根据式(1)，计算能量函数E；

(8) 检查路径的合法性，判断迭代次数是否结束，如果结束，则终止，否则返回到第(4)步；

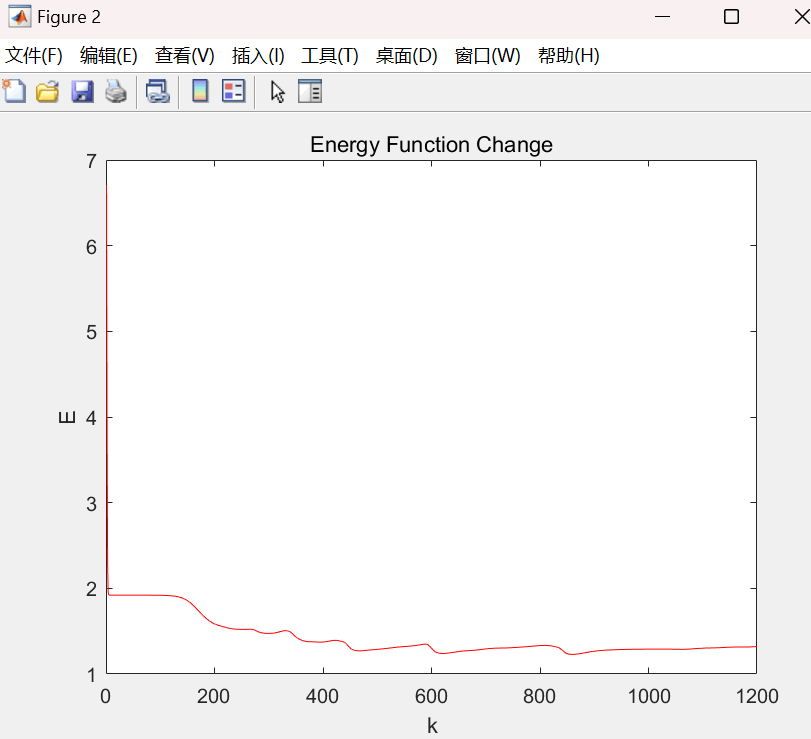
(9) 显示输出迭代次数、最优路径、最优能量函数、路径长度的值，并作出能量函数随时间的变化的曲线图。

四、仿真结果分析

  1. 对程序中的关键代码进行注释与分析。

注释如下：

% TSP Solving by Hopfield Neural Network

function TSP_hopfield()

clear all; % 清除所有工作区变量

close all; % 关闭所有图形窗口

%Step 1: 置初值

A = 1.5; % 设置参数A

D = 1; % 设置参数D

Mu = 30; % 设置参数Mu，用于S函数的斜率

Step = 0.01; % 设置步长，用于更新神经网络的状态

%Step 2: 计算N个城市之间距离, 计算初始路径长度

N = 8; % 设置城市数目

cityfile = fopen('city8.txt', 'rt'); % 打开存储城市坐标的文本文件

cities = fscanf(cityfile, '%f %f', [2, inf]); % 读取城市坐标，二维矩阵，存储为[cities(1,:); cities(2,:)]

fclose(cityfile); % 关闭文件

Initial_Length = Initial_RouteLength(cities); % 计算初始路径长度

DistanceCity = dist(cities', cities); % 计算城市之间的距离矩阵

%Step 3: 神经网络输入的初始化

U = 0.001 * rands(N, N); % 初始化神经网络的状态矩阵U，随机生成一个N×N的矩阵，乘以0.001

V = 1 ./ (1 + exp(-Mu * U)); % 通过S函数将U转换为V

for k = 1:1:1200 % 神经网络优化，迭代2000次

times(k) = k; % 记录当前的迭代次数

%Step 4: 计算du/dt

dU = DeltaU(V, DistanceCity, A, D); % 计算状态矩阵U的变化率dU/dt

%Step 5: 计算u(t)

U = U + dU * Step; % 更新状态矩阵U

%Step 6: 计算网络输出

V = 1 ./ (1 + exp(-Mu * U)); % 通过S函数计算网络输出V

%Step 7: 计算能量函数

E = Energy(V, DistanceCity, A, D); % 计算当前状态下的能量

Ep(k) = E; % 记录每次迭代的能量

%Step 8: 检查路径合法性

[V1, CheckR] = RouteCheck(V); % 检查路径的合法性，确保每行和每列只有一个“1”

end

%Step 9: 显示及作图

if(CheckR == 0) % 如果路径合法（检查路径合法性结果为0）

Final_E = Energy(V1, DistanceCity, A, D); % 计算最终能量

Final_Length = Final_RouteLength(V1, cities); % 计算最终路径长度

disp('迭代次数'); k % 输出迭代次数

disp('寻优路径矩阵'); V1 % 输出最终的路径矩阵

disp('最优能量函数:'); Final_E % 输出最终的能量函数值

disp('初始路程:'); Initial_Length % 输出初始路径长度

disp('最短路程:'); Final_Length % 输出最终优化后的路径长度

PlotR(V1, cities); % 绘制优化后的路径图

else

disp('寻优路径矩阵:'); V1 % 输出寻优路径矩阵

disp('寻优路径无效, 需要重新对神经网络输入进行初始化'); % 输出提示路径无效

end

figure(2); % 创建新图形窗口

plot(times, Ep, 'r'); % 绘制能量变化曲线

title('Energy Function Change'); % 设置标题

xlabel('k'); ylabel('E'); % 设置横纵坐标标签

计算du/dt

function du = DeltaU(V, d, A, D)

[n, n] = size(V); % 获取矩阵V的大小

t1 = repmat(sum(V, 2) - 1, 1, n); % 重复求和后的结果，得到一个矩阵

t2 = repmat(sum(V, 1) - 1, n, 1); % 重复求和后的结果，得到一个矩阵

PermitV = V(:, 2:n); % 获取V的从第二列到最后一列的部分

PermitV = [PermitV, V(:, 1)]; % 在V的末尾添加第一列，形成循环路径

t3 = d * PermitV; % 计算城市之间的距离

du = -1 * (A * t1 + A * t2 + D * t3); % 计算状态更新的变化率

% 标准化路径，并检查路径合法性：要求每行每列只有一个“1”

function [V1, CheckR] = RouteCheck(V)

[rows, cols] = size(V); % 获取矩阵V的行列数

V1 = zeros(rows, cols); % 初始化一个全零的矩阵

[XC, Order] = max(V); % 获取每列最大值的位置，表示每个城市的顺序

for j = 1:cols

V1(Order(j), j) = 1; % 在合法位置填充1，确保每列只有一个1

end

C = sum(V1); % 计算每行和每列的和

R = sum(V1');

CheckR = sumsqr(C - R); % 计算每行和每列和的差值的平方和，检查是否有多于一个1

计算最终总路程

function L = Final_RouteLength(V, cities)

[xxx, order] = max(V); % 获取路径顺序

New = cities(:, order); % 根据路径顺序重新排列城市

New = [New New(:, 1)]; % 形成闭环路径

[rows, cs] = size(New); % 获取路径的行列数

L = 0; % 初始化路径长度

for i = 2:cs

L = L + dist(New(:, i-1)', New(:, i)); % 计算路径的总长度

end

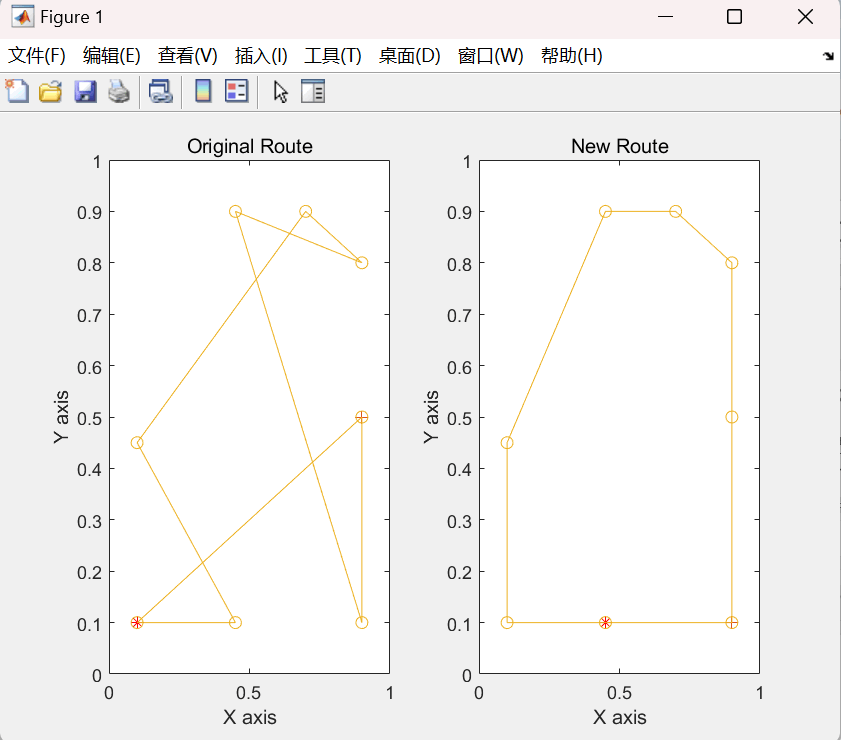
% 路径寻优作图

function PlotR(V, cities)

figure; % 创建新图形窗口

cities = [cities cities(:, 1)]; % 形成闭环路径

[xxx, order] = max(V); % 获取路径顺序

New = cities(:, order); % 根据路径顺序重新排列城市

New = [New New(:, 1)]; % 形成闭环路径

subplot(1, 2, 1); % 创建子图1

plot(cities(1, 1), cities(2, 1), 'r*'); % 绘制第一个城市

hold on;

plot(cities(1, 2), cities(2, 2), '+'); % 绘制第二个城市

hold on;

plot(cities(1,:), cities(2,:), 'o-'); % 绘制城市的原始路径

xlabel('X axis'); ylabel('Y axis');

title('Original Route'); % 设置标题

axis([0, 1, 0, 1]); % 设置坐标轴范围

subplot(1, 2, 2); % 创建子图2

plot(New(1, 1), New(2, 1), 'r*'); % 绘制第一个城市

hold on;

plot(New(1, 2), New(2, 2), '+'); % 绘制第二个城市

hold on;

plot(New(1,:), New(2,:), 'o-'); % 绘制优化后的路径

title('TSP solution');

xlabel('X axis'); ylabel('Y axis'); % 设置坐标轴标签

title('New Route'); % 设置标题

axis([0, 1, 0, 1]); % 设置坐标轴范围

axis on; % 显示坐标轴

  1. 按照实验步骤获得仿真实验结果

实验结果如下：

05publishedweb/W002-学习进度/DocxerAttachments/Attachment 10.png

05publishedweb/W002-学习进度/DocxerAttachments/Attachment 11.png

TSP_hopfiled

迭代次数

k =

1200

寻优路径矩阵

V1 =

0 0 0 0 1 0 0 0

0 0 0 0 0 0 0 1

0 0 0 0 0 0 1 0

0 0 1 0 0 0 0 0

1 0 0 0 0 0 0 0

0 1 0 0 0 0 0 0

0 0 0 1 0 0 0 0

0 0 0 0 0 1 0 0

最优能量函数:

Final_E =

1.4468

初始路程:

Initial_Length =

4.1419

最短路程:

Final_Length =

2.8937

**3.**分析网络参数的选取对网络性能的影响。

Hopfield网络的性能会受到多个参数的影响，主要包括以下几个方面：

神经元数量的增加会影响网络的存储能力和计算效率。过多的神经元可能导致网络存储能力超限，影响模式的恢复效果。

Hopfield网络常用的学习规则是Hebb规则或伪逆学习规则，不同的学习规则会对网络的收敛速度和稳定性产生影响。合理的学习规则有助于网络快速收敛，并避免陷入局部极小值。

每个神经元的激活阈值决定了神经元是否被激活。阈值的选择直接影响网络的激活函数和模式识别能力。如果阈值设置过低或过高，可能导致神经元的激活过于极端，影响网络的表现。

Hopfield网络的连接矩阵影响着网络的动力学行为。全连接网络和部分连接网络在性能上有所不同。全连接网络可以更好地进行信息传播和存储，但计算开销较大，而部分连接网络可能会提升计算效率，但会在模式恢复能力上有所牺牲。

五、思考题

  1. Hopfield神经网络中神经元的个数是否越多越好？

在Hopfield神经网络中，神经元的个数并不是越多越好。网络的性能与神经元数量有一定关系，但过多的神经元可能会导致以下问题：

每增加一个神经元，Hopfield网络的状态空间和计算复杂度都会指数级增长。这使得网络的运行效率降低，尤其是在需要进行大量迭代的情况下。

Hopfield神经网络的存储容量有限。理论上，网络能存储的稳定模式数目是神经元个数的一个上限，约为神经元个数的1/2，即网络最多可以存储大约 N/2 个模式，其中 NN 是神经元个数。如果神经元太多，网络的存储能力会饱和，存储的模式可能会互相干扰，导致性能下降。

2. 权值的初始值是否影响网络的优化性能？为什么？

在Hopfield神经网络中，权值的初始值对网络的优化性能是有影响的，尤其是在网络初始化和收敛性方面。

如果权值初始化不当，可能会导致网络收敛到局部极小值，影响网络的优化能力。初始化的好坏直接影响网络能否找到正确的稳定模式。例如，如果权值过大或过小，可能会使神经元的激活过于极端，导致网络无法收敛到稳定态。

合理的权值初始化有助于网络以更快的速度找到一个收敛解。如果初始权值设置合理，网络可以更快地逼近正确的解；否则，可能需要更多的时间来迭代并进行调整。

3. 能量函数的选取需考虑哪些因素？

能量函数应当能够反映网络的稳定性，即一个稳定的网络状态对应一个局部最小值。网络在进行模式识别或优化任务时，应当逐步降低能量，直到达到全局或局部最低点。

能量函数的形式应该便于计算和更新。在实际应用中，能量函数的计算复杂度应当尽可能低，以提高网络的运行效率。

能量函数应该与网络的目标任务紧密相关。

理想的能量函数设计应确保网络的状态最终会收敛至最优解。一个设计不当的能量函数可能会导致网络收敛到局部极小值，影响网络性能。

六、心得体会

在实际实验过程中，使用Hopfield神经网络进行模式识别和优化任务时，以下几点值得注意：

在实验中通过不同形式的能量函数进行测试，发现选择合适的能量函数对网络性能至关重要。能量函数的设计要确保网络能够快速收敛到正确的解，且能量下降过程必须稳定。

Hopfield网络的收敛性是其核心特性之一。在实验中观察到，网络能有效地恢复学习过的模式，但若存储的模式过多，恢复过程的准确性会下降。因此，适当控制存储模式的数量是提高网络性能的关键。

Hopfield神经网络在实际应用中非常依赖于参数设置和网络结构设计，合理的调整可以显著提高其优化性能和模式识别能力。

评 语：

指导老师： 日 期：