241123_-1_进度搬运_第4个校园团队项目_医学X射线成像下肢手术方案预测自回归分析模型
天津工业大学
控制科学与工程学院
实
验
报
告
课程名称: 模式识别与机器学习
上课时间:2024至2025学年(春/秋)学期
班 级: 自动化2202
姓 名: 陈星佟
学 号: 2210410224
评 分:
一、实验目的
(1)正文宋体四号,首行缩进2字符,单倍行距;
(2)图片需进行标号,如“图1 实验电路图”,宋体小四居中;
(3)表格需进行标号,如“表1 实验结果”,三线表宋体小四;
(4)实验目的参考实验指导书。
使用下肢全长X射线相关尺寸和角度数据集样本训练模型,能对测试样本中的手术方案进行分类预测,通过回归分析对手术角度进行预测,并根据该样本的实际标签来检验预测的效果。
二、实验内容
数据预处理
调整数据格式
由于数据中混合了字符串和数字,不能用MATLAB直接处理,需要先统一数据格式,将手术类型转换为数字代表,将角度值从字符串中提取出来。
导入数据
data = readtable('诊断数据.xlsx');
将第14列数据转化为标签
data_labels = cellfun(@(x) label_map(x), data{:, 14}, 'UniformOutput', true);
将处理后的数据添加到数据表
data{:, 14} = num2cell(data_labels); % 用转换后的标签替换第14列
data{:, 15} = num2cell(data_angles); % 用提取的数字替换第15列
测试集的数据按照训练集的归一化方式进行归一化。
做回归分析时,需要考虑标签值的归一化和预测结果的反归一化,反归一化方法如下:
T_sim1 = mapminmax('reverse', t_sim1, ps_output);第14列是手术方案
M = size(P_train, 2);
P_test = data(temp(m*0.8+1: end), 2: 13)';
T_test = data(temp(m*0.8+1: end), 14)';
N = size(P_test, 2);
tc = fitctree(p_train',T_train','MaxNumSplits',11);显示决策树结构
Y_pred = predict(tc,p_test');
accuracy = sum(Y_pred == T_test') / length(T_test) * 100;
- 记录数据
| 决策树 | ||||
| 决策树分支 | 自动(请在此处填写默认的分支数,例如300) | 7 | 15 | 35 |
| 预测准确率 | 87.6344% | 51.8717% | 74.1935% | 83% |
请分别记录以上实验的混淆矩阵图、决策树结构图。
混淆矩阵图示例:
figure;
cm = confusionchart(T_test',Y_pred)
cm.ColumnSummary = 'column-normalized';
cm.Title = '预测结果,班级-姓名-学号';
(三)SVM分类
使用SVM分类函数进行实验。
model = fitcecoc(train_data,train_label);
第15列是角度信息
M = size(P_train, 2);
P_test = data(temp(m*0.8+1: end), 2: 13)';
T_test = data(temp(m*0.8+1: end), 15)';
N = size(P_test, 2);
不要设置太大,否则很慢
数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
绘图
figure
plot(1: N, T_test, 'r-', 1: N, T_sim1, 'b-', 'LineWidth', 1)
legend('真实值','预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比,班级-姓名-学号';['RMSE=' num2str(error1)]};
title(string)
xlim([1, N])
grid
保存图像。
(4)网络优化
可截图保存网络结构
设置3层不同神经元数量的网络
net.layers{1}.transferFcn = 'tansig';%设置每一层的激活函数,正切S型函数
net.layers{2}.transferFcn = 'purelin';%线性函数
net.layers{3}.transferFcn = 'logsig';%对数S型函数
net = train(net, p_train, t_train);
还可调整训练参数,请自行设计一个BP神经网络,实现均方根误差小于6.5,保留网络结构图和最终结果图。
三、实验步骤
BPNNfangan2.m
warning off
close all
clear
clc
data = readtable('诊断数据2.xlsx');
[m, ~] = size(data);
temp = 1:1:m;
P_train = table2array(data(temp(1:floor(m * 0.8)), 2:13))';
T_train = table2array(data(temp(1:floor(m * 0.8)), 14))';
M = size(P_train, 2);
P_test = table2array(data(temp(floor(m * 0.8) + 1:end), 2:13))';
T_test = table2array(data(temp(floor(m * 0.8) + 1:end), 14))';
N = size(P_test, 2);
[P_train_norm, ps_input] = mapminmax(P_train, 0, 1);
P_test_norm = mapminmax('apply', P_test, ps_input);
T_train_onehot = zeros(M, 6);
for i = 1:M
T_train_onehot(i, T_train(i) + 1) = 1;
end
net = patternnet([50, 30, 10]);
net.trainParam.epochs = 500;
net.trainParam.goal = 1e-6;
net.trainParam.lr = 0.01;
net.performFcn = 'crossentropy';
net.layers{1}.transferFcn = 'tansig';
net.layers{2}.transferFcn = 'logsig';
net.layers{3}.transferFcn = 'softmax';
disp('开始训练 BP 神经网络...');
net = train(net, P_train_norm, T_train_onehot');
save('BP_model_classification.mat', 'net');
disp('BP 神经网络模型已保存为文件:BP_model_classification.mat');
disp('开始测试 BP 神经网络...');
Y_pred = net(P_test_norm);
T_pred = vec2ind(Y_pred) - 1;
accuracy = sum(T_pred == T_test) / N * 100;
rmse = sqrt(mean((T_pred - T_test).^2));
disp(['测试集预测准确率: ', num2str(accuracy), '%']);
disp(['测试集均方根误差 RMSE: ', num2str(rmse)]);
figure;
plot(1:N, T_test, 'r-', 1:N, T_pred, 'b-', 'LineWidth', 1);
legend('真实值', '预测值');
xlabel('样本编号');
ylabel('分类标签');
title({'测试集分类结果折线图,班级:自动化2202-姓名:陈星佟-学号:2210410224'; ['准确率 = ', num2str(accuracy), '%, RMSE = ', num2str(rmse)]});
grid on;
saveas(gcf, 'BP_Test_Classification_LinePlot.png');
disp('分类结果折线图已保存为文件:BP_Test_Classification_LinePlot.png');
correct_predictions = sum(T_pred == T_test);
incorrect_predictions = N - correct_predictions;
figure;
pie([correct_predictions, incorrect_predictions], {'正确预测', '错误预测'});
title({'预测结果分布饼图,班级:自动化2202-姓名:陈星佟-学号:2210410224'; ['准确率 = ', num2str(accuracy), '%']});
saveas(gcf, 'BP_Test_Classification_PieChart.png');
disp('预测结果分布饼图已保存为文件:BP_Test_Classification_PieChart.png');
disp('神经网络结构详情:');
disp(net);
view(net);
disp('绘制神经网络内部结构详细图...');
figure;
hold on;
layer_positions = [0, 1, 2, 3];
layer_neurons = [size(P_train_norm, 1), 50, 30, 10, size(T_train_onehot, 2)];
colors = ['r', 'g', 'b', 'm'];
node_radius = 0.1;
for l = 1:length(layer_positions)
for n = 1:layer_neurons(l)
rectangle('Position', [layer_positions(l) - node_radius, n - node_radius, 2 * node_radius, 2 * node_radius], ...
'Curvature', [1, 1], 'EdgeColor', colors(min(l, length(colors))), ...
'FaceColor', colors(min(l, length(colors))));
end
end
for l = 1:(length(layer_positions) - 1)
for n1 = 1:layer_neurons(l)
for n2 = 1:layer_neurons(l + 1)
line([layer_positions(l), layer_positions(l + 1)], [n1, n2], 'Color', 'k', 'LineWidth', 0.5);
end
end
end
text(-0.5, mean(1:layer_neurons(1)), '输入层', 'FontSize', 12, 'HorizontalAlignment', 'center');
text(0.5, mean(1:layer_neurons(2)), '隐藏层1', 'FontSize', 12, 'HorizontalAlignment', 'center');
text(1.5, mean(1:layer_neurons(3)), '隐藏层2', 'FontSize', 12, 'HorizontalAlignment', 'center');
text(2.5, mean(1:layer_neurons(4)), '隐藏层3', 'FontSize', 12, 'HorizontalAlignment', 'center');
text(3.5, mean(1:layer_neurons(5)), '输出层', 'FontSize', 12, 'HorizontalAlignment', 'center');
title('BP 神经网络结构详细图');
xlabel('层编号');
ylabel('神经元编号');
grid on;
hold off;
saveas(gcf, 'BP_Network_Structure_Detail_with_Nodes.png');
disp('BP 神经网络结构详细图(带节点)已保存为文件:BP_Network_Structure_Detail_with_Nodes.png');
residuals = T_test - T_pred;
figure;
scatter(1:N, residuals, 'b', 'filled');
hold on;
plot(1:N, zeros(1, N), 'r--', 'LineWidth', 1.5);
p = polyfit(1:N, residuals, 2);
y_fit = polyval(p, 1:N);
plot(1:N, y_fit, 'g-', 'LineWidth', 1.5);
hold off;
xlabel('样本编号');
ylabel('残差');
title({'残差散点图及拟合曲线 (实际值 - 预测值)', '班级:自动化2202-姓名:陈星佟-学号:2210410224'});
legend('残差散点', '零误差线', '拟合曲线');
grid on;
saveas(gcf, 'BP_Residual_Scatter_Fit_Plot.png');
disp('残差散点图及拟合曲线已保存为文件:BP_Residual_Scatter_Fit_Plot.png');
figure;
histogram(residuals, 'BinWidth', 1, 'FaceColor', 'g');
xlabel('残差');
ylabel('频率');
title({'残差直方图', '班级:自动化2202-姓名:陈星佟-学号:2210410224'});
grid on;
saveas(gcf, 'BP_Residual_Histogram.png');
disp('残差直方图已保存为文件:BP_Residual_Histogram.png');
if accuracy < 70
disp('预测准确率低于 70%,建议调整以下参数:');
disp('- 增加网络层数或神经元数');
disp('- 调整学习率');
disp('- 使用更多数据进行训练');
else
disp('模型预测准确率已达到 70%以上。');
end
BPNNfangan.m
warning off
close all
clear
clc
data = readtable('诊断数据2.xlsx');
[m, ~] = size(data);
temp = 1:1:m;
P_train = table2array(data(temp(1:floor(m * 0.8)), 2:13))';
T_train = table2array(data(temp(1:floor(m * 0.8)), 15))';
M = size(P_train, 2);
P_test = table2array(data(temp(floor(m * 0.8) + 1:end), 2:13))';
T_test = table2array(data(temp(floor(m * 0.8) + 1:end), 15))';
N = size(P_test, 2);
[P_train_norm, ps_input] = mapminmax(P_train, 0, 1);
[T_train_norm, ps_output] = mapminmax(T_train, 0, 1);
P_test_norm = mapminmax('apply', P_test, ps_input);
T_test_norm = mapminmax('apply', T_test, ps_output);
net = feedforwardnet(50);
net.trainParam.epochs = 200;
net.trainParam.goal = 1e-7;
net.trainParam.lr = 0.01;
net.layers{1}.transferFcn = 'tansig';
net.layers{2}.transferFcn = 'purelin';
net.trainFcn = 'trainlm';
disp('开始训练 BP 神经网络...');
net = train(net, P_train_norm, T_train_norm);
save('BP_model.mat', 'net');
disp('BP 神经网络模型已保存为文件:BP_model.mat');
disp('开始测试 BP 神经网络...');
T_sim_norm = net(P_test_norm);
T_sim = mapminmax('reverse', T_sim_norm, ps_output);
error_rmse = sqrt(sum((T_sim - T_test).^2) ./ N);
disp(['均方根误差 RMSE: ', num2str(error_rmse)]);
figure;
plot(1:N, T_test, 'r-', 1:N, T_sim, 'b-', 'LineWidth', 1);
legend('真实值', '预测值');
xlabel('预测样本');
ylabel('预测结果');
title({'测试集预测结果对比,班级:自动化2202-姓名:陈星佟-学号:2210410224'; ['RMSE = ', num2str(error_rmse)]});
xlim([1, N]);
grid;
saveas(gcf, 'BP_Test_Result.png');
disp('预测结果图已保存为文件:BP_Test_Result.png');
view(net);
disp('请截图保存网络结构图');
disp('开始优化 BP 神经网络...');
optimized_net = feedforwardnet([50, 20, 10]);
optimized_net.layers{1}.transferFcn = 'tansig';
optimized_net.layers{2}.transferFcn = 'purelin';
optimized_net.layers{3}.transferFcn = 'logsig';
optimized_net.trainParam.epochs = 300;
optimized_net.trainParam.goal = 1e-7;
optimized_net.trainParam.lr = 0.005;
optimized_net = train(optimized_net, P_train_norm, T_train_norm);
T_sim_optimized_norm = optimized_net(P_test_norm);
T_sim_optimized = mapminmax('reverse', T_sim_optimized_norm, ps_output);
error_rmse_optimized = sqrt(sum((T_sim_optimized - T_test).^2) ./ N);
disp(['优化后均方根误差 RMSE: ', num2str(error_rmse_optimized)]);
figure;
plot(1:N, T_test, 'r-', 1:N, T_sim_optimized, 'b-', 'LineWidth', 1);
legend('真实值', '优化后预测值');
xlabel('预测样本');
ylabel('预测结果');
title({'优化后测试集预测结果对比,班级:自动化2202-姓名:陈星佟-学号:2210410224'; ['RMSE = ', num2str(error_rmse_optimized)]});
xlim([1, N]);
grid;
saveas(gcf, 'BP_Optimized_Test_Result.png');
disp('优化后预测结果图已保存为文件:BP_Optimized_Test_Result.png');
residuals = T_test - T_sim;
figure;
scatter(1:N, residuals, 'b', 'filled');
hold on;
plot(1:N, zeros(1, N), 'r--', 'LineWidth', 1.5);
p = polyfit(1:N, residuals, 2);
y_fit = polyval(p, 1:N);
plot(1:N, y_fit, 'g-', 'LineWidth', 1.5);
hold off;
xlabel('样本编号');
ylabel('残差');
title({'残差散点图及拟合曲线 (实际值 - 预测值)', '班级:自动化2202-姓名:陈星佟-学号:2210410224'});
legend('残差散点', '零误差线', '拟合曲线');
grid on;
saveas(gcf, 'BP_Residual_Scatter_Fit_Plot.png');
disp('残差散点图及拟合曲线已保存为文件:BP_Residual_Scatter_Fit_Plot.png');
figure;
histogram(residuals, 'BinWidth', 1, 'FaceColor', 'g');
xlabel('残差');
ylabel('频率');
title({'残差直方图', '班级:自动化2202-姓名:陈星佟-学号:2210410224'});
grid on;
saveas(gcf, 'BP_Residual_Histogram.png');
disp('残差直方图已保存为文件:BP_Residual_Histogram.png');
disp('计算优化后模型的准确率...');
T_sim_optimized_class = round(T_sim_optimized);
T_test_class = round(T_test);
optimized_accuracy = sum(T_sim_optimized_class == T_test_class) / length(T_test_class) * 100;
disp(['优化后模型的准确率: ', num2str(optimized_accuracy), '%']);
view(optimized_net);
disp('请截图保存网络结构图');
guiyihua_2.m
warning off
close all
clear
clc
data = readtable('诊断数据2.xlsx');
[m, n] = size(data);
temp = 1:1:m;
P_train = data{temp(1: floor(m * 0.8)), 2:13}';
T_train = data{temp(1: floor(m * 0.8)), 14}';
M = size(P_train, 2);
P_test = data{temp(floor(m * 0.8) + 1: end), 2:13}';
T_test = data{temp(floor(m * 0.8) + 1: end), 14}';
N = size(P_test, 2);
normalize = @(x) (x - min(x(:))) / (max(x(:)) - min(x(:)));
P_train_normalized = normalize(P_train);
P_test_normalized = normalize(P_test);
disp('归一化后的训练集特征:');
disp(P_train_normalized);
disp('归一化后的测试集特征:');
disp(P_test_normalized);
P_train_normalized_table = array2table(P_train_normalized', 'VariableNames', data.Properties.VariableNames(2:13));
P_test_normalized_table = array2table(P_test_normalized', 'VariableNames', data.Properties.VariableNames(2:13));
train_output = [P_train_normalized_table, table(T_train', 'VariableNames', {'Label'})];
test_output = [P_test_normalized_table, table(T_test', 'VariableNames', {'Label'})];
writetable(train_output, '训练集_归一化结果.xlsx');
writetable(test_output, '测试集_归一化结果.xlsx');
disp('归一化数据已保存到文件:训练集_归一化结果.xlsx 和 测试集_归一化结果.xlsx');
yuchuli_1.m
warning off
close all
clear
clc
data = readtable('诊断数据.xlsx');
label_map = containers.Map({'NeceBihe_DFO_SmoothL1_coslr', 'Neicebihe_HTO_SmoothL1_coslr', ...
'NeiceOpen_HTO_SmoothL1_coslr', 'WaiceBihe_DFO_smoothL1_coslr', ...
'WaiceOpen_DFO_smoothL1', 'WaiceOpen_HTO_SmoothL1_coslr'}, ...
[0, 1, 2, 3, 4, 5]);
data_labels = cellfun(@(x) label_map(x), data{:, 14}, 'UniformOutput', true);
data_angles = cellfun(@(x) regexp(x, 'Rectify [Aa]ngle: (\d+(.\d+)?) degrees', 'tokens'), data{:, 15}, 'UniformOutput', false);
data_angles = cellfun(@(x) str2double(x{1}{1}), data_angles);
data{:, 14} = num2cell(data_labels);
data{:, 15} = num2cell(data_angles);
outputfile ='诊断数据2.xlsx';
writetable(data,outputfile);
SVMfangan2.m
warning off
close all
clear
clc
train_data = readtable('训练集_归一化结果.xlsx');
test_data = readtable('测试集_归一化结果.xlsx');
P_train = table2array(train_data(:, 1:end-1));
T_train = table2array(train_data(:, end));
P_test = table2array(test_data(:, 1:end-1));
T_test = table2array(test_data(:, end));
disp('开始训练 SVM 模型...');
t = templateSVM('Standardize', true, 'KernelFunction', 'polynomial');
model = fitcecoc(P_train, T_train, 'Learners', t);
save('SVM_model_2.mat', 'model');
disp('SVM 模型已保存为文件:SVM_model_2.mat');
disp('开始测试模型...');
Y_train_pred = predict(model, P_train);
Y_test_pred = predict(model, P_test);
train_accuracy = sum(Y_train_pred == T_train) / length(T_train) * 100;
test_accuracy = sum(Y_test_pred == T_test) / length(T_test) * 100;
disp(['训练集预测准确率: ', num2str(train_accuracy), '%']);
disp(['测试集预测准确率: ', num2str(test_accuracy), '%']);
if train_accuracy - test_accuracy > 20
disp('模型可能过拟合。');
overfitting_probability = (train_accuracy - test_accuracy) / train_accuracy * 100;
disp(['过拟合概率: ', num2str(overfitting_probability), '%']);
elseif train_accuracy < 70 && test_accuracy < 70
disp('模型可能欠拟合。');
underfitting_probability = 100 - max(train_accuracy, test_accuracy);
disp(['欠拟合概率: ', num2str(underfitting_probability), '%']);
else
disp('模型拟合正常。');
end
disp('绘制混淆矩阵图...');
figure;
cm = confusionchart(Y_test_pred, T_test);
cm.ColumnSummary = 'column-normalized';
cm.XLabel = '真实类';
cm.YLabel = '预测类';
cm.Title = 'SVM 分类结果 - 混淆矩阵图;班级:自动化2202-姓名:陈星佟-学号:2210410224';
disp('SVM 分类实验完成。');
SVMfangan.m
warning off
close all
clear
clc
data = readtable('诊断数据2.xlsx');
P = table2array(data(:, 2:13));
T = table2array(data(:, 14));
[m, ~] = size(P);
train_ratio = 0.7;
train_index = 1:floor(m * train_ratio);
test_index = (floor(m * train_ratio) + 1):m;
P_train = P(train_index, :);
T_train = T(train_index);
P_test = P(test_index, :);
T_test = T(test_index);
disp('开始训练 SVM 模型...');
t = templateSVM('Standardize', true, 'KernelFunction', 'linear');%linear gaussian polynomial
model = fitcecoc(P_train, T_train, 'Learners', t);
save('SVM_model.mat', 'model');
disp('SVM 模型已保存为文件:SVM_model.mat');
disp('开始测试模型...');
Y_train_pred = predict(model, P_train);
Y_test_pred = predict(model, P_test);
train_accuracy = sum(Y_train_pred == T_train) / length(T_train) * 100;
test_accuracy = sum(Y_test_pred == T_test) / length(T_test) * 100;
disp(['训练集预测准确率: ', num2str(train_accuracy), '%']);
disp(['测试集预测准确率: ', num2str(test_accuracy), '%']);
if train_accuracy - test_accuracy > 20
disp('模型可能过拟合。');
overfitting_probability = (train_accuracy - test_accuracy) / train_accuracy * 100;
disp(['过拟合概率: ', num2str(overfitting_probability), '%']);
elseif train_accuracy < 70 && test_accuracy < 70
disp('模型可能欠拟合。');
underfitting_probability = 100 - max(train_accuracy, test_accuracy);
disp(['欠拟合概率: ', num2str(underfitting_probability), '%']);
else
disp('模型拟合正常。');
end
disp('绘制混淆矩阵图...');
figure;
cm = confusionchart(Y_test_pred, T_test);
cm.ColumnSummary = 'column-normalized';
cm.XLabel = '真实类';
cm.YLabel = '预测类';
cm.Title = 'SVM 分类结果 - 混淆矩阵图;班级:自动化2202-姓名:陈星佟-学号:2210410224';
disp('SVM 分类实验完成。');
DecisionTree_3.m
warning off
close all
clear
clc
train_data = readtable('训练集_归一化结果.xlsx');
test_data = readtable('测试集_归一化结果.xlsx');
P_train = table2array(train_data(:, 1:end-1))';
T_train = table2array(train_data(:, end))';
P_test = table2array(test_data(:, 1:end-1))';
T_test = table2array(test_data(:, end))';
tc = fitctree(P_train', T_train', 'MaxNumSplits', 35);
view(tc, 'Mode', 'graph');
Y_train_pred = predict(tc, P_train');
Y_test_pred = predict(tc, P_test');
train_accuracy = sum(Y_train_pred == T_train') / length(T_train) * 100;
test_accuracy = sum(Y_test_pred == T_test') / length(T_test) * 100;
disp(['训练集预测准确率: ', num2str(train_accuracy), '%']);
disp(['测试集预测准确率: ', num2str(test_accuracy), '%']);
if train_accuracy - test_accuracy > 20
disp('模型可能过拟合。');
overfitting_probability = (train_accuracy - test_accuracy) / train_accuracy * 100;
disp(['过拟合概率: ', num2str(overfitting_probability), '%']);
elseif train_accuracy < 70 && test_accuracy < 70
disp('模型可能欠拟合。');
underfitting_probability = 100 - max(train_accuracy, test_accuracy);
disp(['欠拟合概率: ', num2str(underfitting_probability), '%']);
else
disp('模型拟合正常。');
end
figure;
cm = confusionchart(Y_test_pred, T_test');
cm.ColumnSummary = 'column-normalized';
cm.XLabel = '真实类';
cm.YLabel = '预测类';
cm.Title = '预测结果,班级:自动化2202-姓名:陈星佟-学号:2210410224';
output_table = table((1:length(T_test))', T_test', Y_test_pred, ...
'VariableNames', {'样本编号', '真实标签', '预测标签'});
writetable(output_table, '决策树方案_测试集预测结果.xlsx');
disp('测试集预测结果已保存到文件:决策树方案_测试集预测结果.xlsx');
DecisionTree_prune.m
warning off
close all
clear
clc
train_data = readtable('训练集_归一化结果.xlsx');
test_data = readtable('测试集_归一化结果.xlsx');
P_train = table2array(train_data(:, 1:end-1));
T_train = table2array(train_data(:, end));
P_test = table2array(test_data(:, 1:end-1));
T_test = table2array(test_data(:, end));
disp('训练决策树模型...');
tc = fitctree(P_train, T_train, 'MaxNumSplits', 35);
[subTreeLosses, subTreeDepths] = loss(tc, P_train, T_train, 'SubTrees', 'all');
[~, bestIdx] = min(subTreeLosses);
bestLevel = subTreeDepths(bestIdx);
tc_pruned = prune(tc, 'Level', bestLevel);
disp(['剪枝后的最优树深度: ', num2str(bestLevel)]);
view(tc_pruned, 'Mode', 'graph');
disp('开始预测...');
Y_train_pred = predict(tc_pruned, P_train);
Y_test_pred = predict(tc_pruned, P_test);
train_accuracy = sum(Y_train_pred == T_train) / length(T_train) * 100;
test_accuracy = sum(Y_test_pred == T_test) / length(T_test) * 100;
disp(['训练集预测准确率: ', num2str(train_accuracy), '%']);
disp(['测试集预测准确率: ', num2str(test_accuracy), '%']);
if train_accuracy - test_accuracy > 20
disp('模型可能过拟合。');
overfitting_probability = (train_accuracy - test_accuracy) / train_accuracy * 100;
disp(['过拟合概率: ', num2str(overfitting_probability), '%']);
elseif train_accuracy < 70 && test_accuracy < 70
disp('模型可能欠拟合。');
underfitting_probability = 100 - max(train_accuracy, test_accuracy);
disp(['欠拟合概率: ', num2str(underfitting_probability), '%']);
else
disp('模型拟合正常。');
end
disp('绘制混淆矩阵图...');
figure;
cm = confusionchart(Y_test_pred, T_test);
cm.ColumnSummary = 'column-normalized';
cm.XLabel = '真实类';
cm.YLabel = '预测类';
cm.Title = '剪枝后的决策树分类结果';
disp('保存预测结果...');
output_table = table((1:length(T_test))', T_test, Y_test_pred, ...
'VariableNames', {'样本编号', '真实标签', '预测标签'});
writetable(output_table, '决策树剪枝方案_测试集预测结果.xlsx');
disp('测试集预测结果已保存到文件:决策树剪枝方案_测试集预测结果.xlsx');
DecisionTreePCA.m
warning off
close all
clear
clc
train_data = readtable('训练集_归一化结果.xlsx');
test_data = readtable('测试集_归一化结果.xlsx');
P_train = table2array(train_data(:, 1:end-1));
T_train = table2array(train_data(:, end));
P_test = table2array(test_data(:, 1:end-1));
T_test = table2array(test_data(:, end));
disp('开始执行 PCA 降维...');
[coeff, score_train, latent, tsquared, explained] = pca(P_train);
disp('PCA 解释的方差比例 (%):');
disp(explained);
disp(['前 2 个主成分累计解释方差比例: ', num2str(sum(explained(1:2))), '%']);
disp(['前 3 个主成分累计解释方差比例: ', num2str(sum(explained(1:3))), '%']);
n_components = find(cumsum(explained) >= 95, 1);
disp(['选择的主成分数目: ', num2str(n_components)]);
P_train_pca = score_train(:, 1:n_components);
P_test_pca = (P_test - mean(P_train)) * coeff(:, 1:n_components);
disp('PCA 降维后的训练集特征:');
disp(P_train_pca(1:5, :));
disp('PCA 降维后的测试集特征:');
disp(P_test_pca(1:5, :));
tc = fitctree(P_train_pca, T_train, 'MaxNumSplits', 35);
view(tc, 'Mode', 'graph');
Y_test_pred = predict(tc, P_test_pca);
train_accuracy = sum(predict(tc, P_train_pca) == T_train) / length(T_train) * 100;
test_accuracy = sum(Y_test_pred == T_test) / length(T_test) * 100;
disp(['训练集预测准确率: ', num2str(train_accuracy), '%']);
disp(['测试集预测准确率: ', num2str(test_accuracy), '%']);
if train_accuracy - test_accuracy > 20
disp('模型可能过拟合。');
overfitting_probability = (train_accuracy - test_accuracy) / train_accuracy * 100;
disp(['过拟合概率: ', num2str(overfitting_probability), '%']);
elseif train_accuracy < 70 && test_accuracy < 70
disp('模型可能欠拟合。');
underfitting_probability = 100 - max(train_accuracy, test_accuracy);
disp(['欠拟合概率: ', num2str(underfitting_probability), '%']);
else
disp('模型拟合正常。');
end
figure;
cm = confusionchart(Y_test_pred, T_test);
cm.ColumnSummary = 'column-normalized';
cm.XLabel = '真实类';
cm.YLabel = '预测类';
cm.Title = '预测结果,班级:自动化2202-姓名:陈星佟-学号:2210410224';
output_table = table((1:length(T_test))', T_test, Y_test_pred, ...
'VariableNames', {'样本编号', '真实标签', '预测标签'});
writetable(output_table, '决策树+PCA_测试集预测结果.xlsx');
disp('PCA 降维后的测试集预测结果已保存到文件:决策树+PCA_测试集预测结果.xlsx');
所有工程文件和代码:链接: https://pan.baidu.com/s/1FaislcXYXZP46Jv96V-MFw?pwd=ix1s 提取码: ix1s 复制这段内容后打开百度网盘手机App,操作更方便哦
--来自百度网盘超级会员v6的分享
四、实验结果
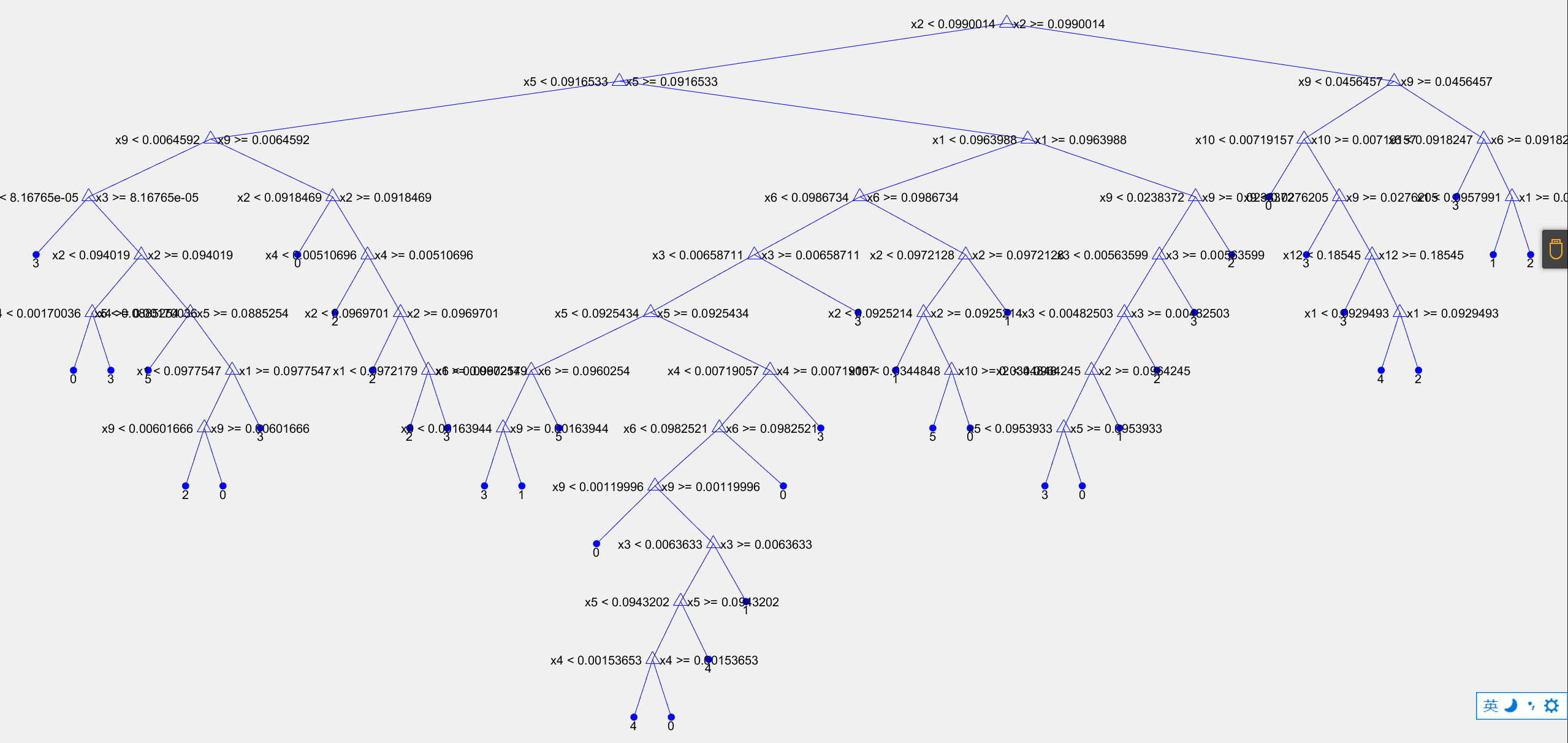
图1:决策树方案:分支=300 决策树结构图
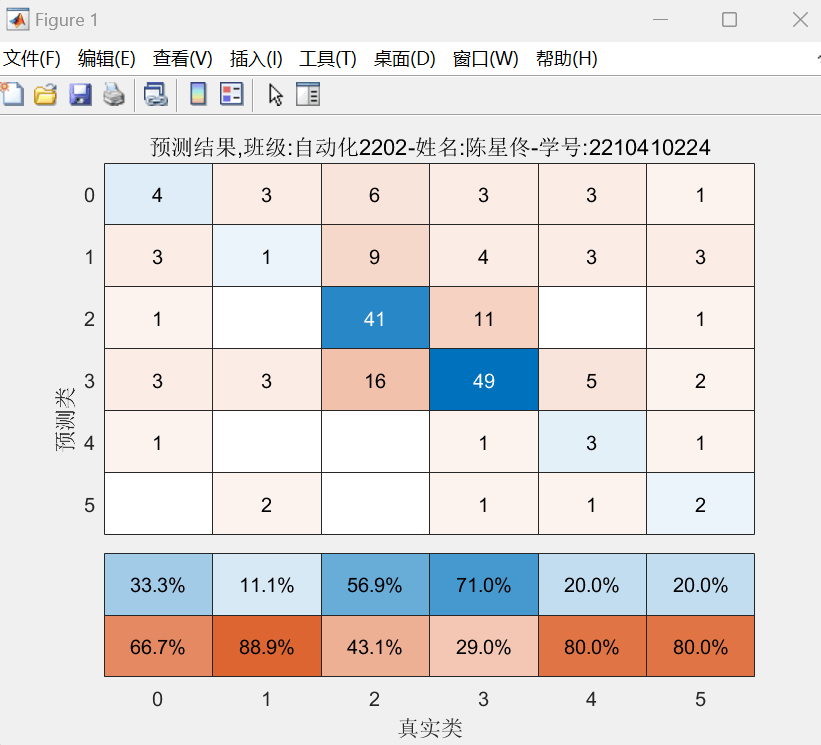
图2:决策树方案:分支=300 混淆矩阵图
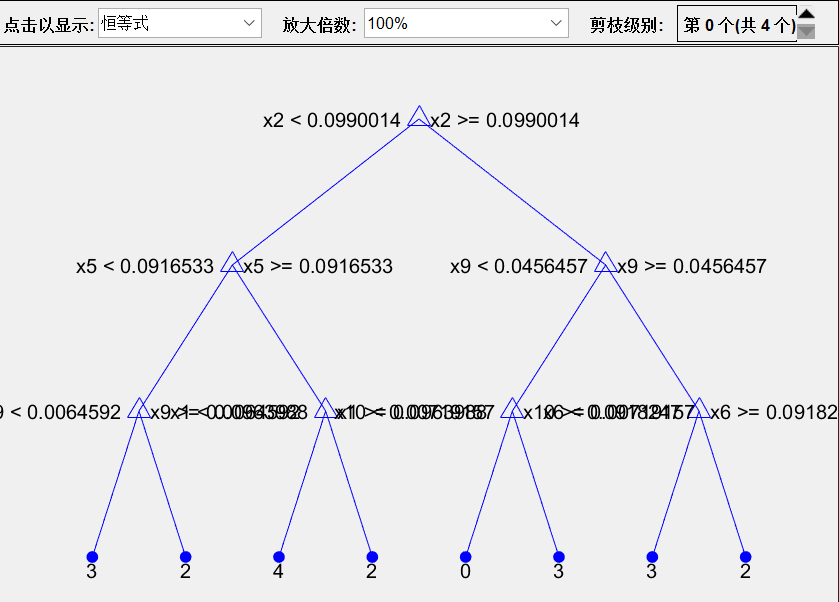
图3:决策树方案:分支=7 决策树结构图
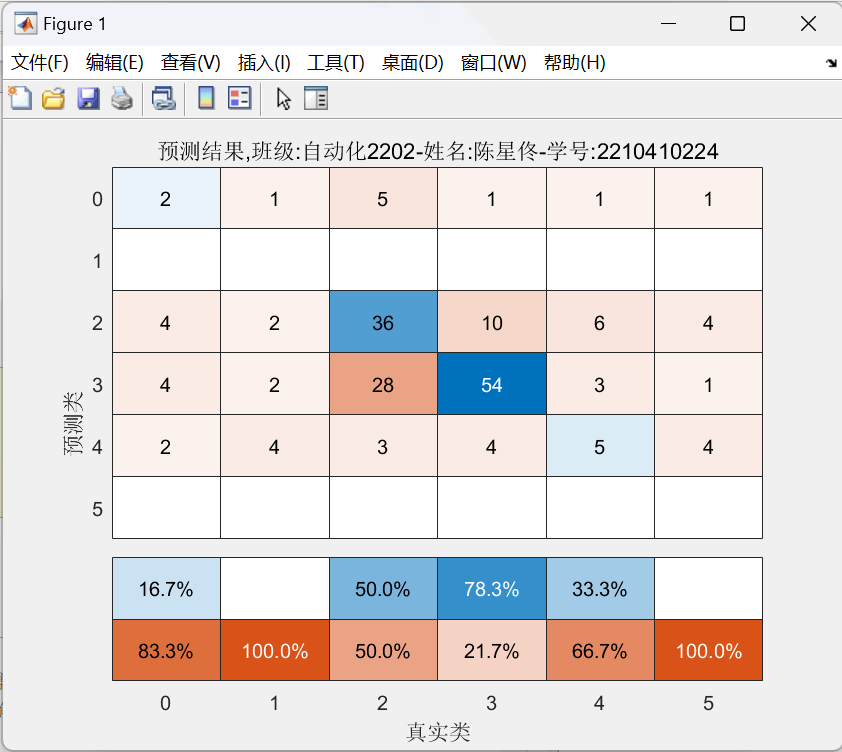
图4:决策树方案:分支=7 混淆矩阵图
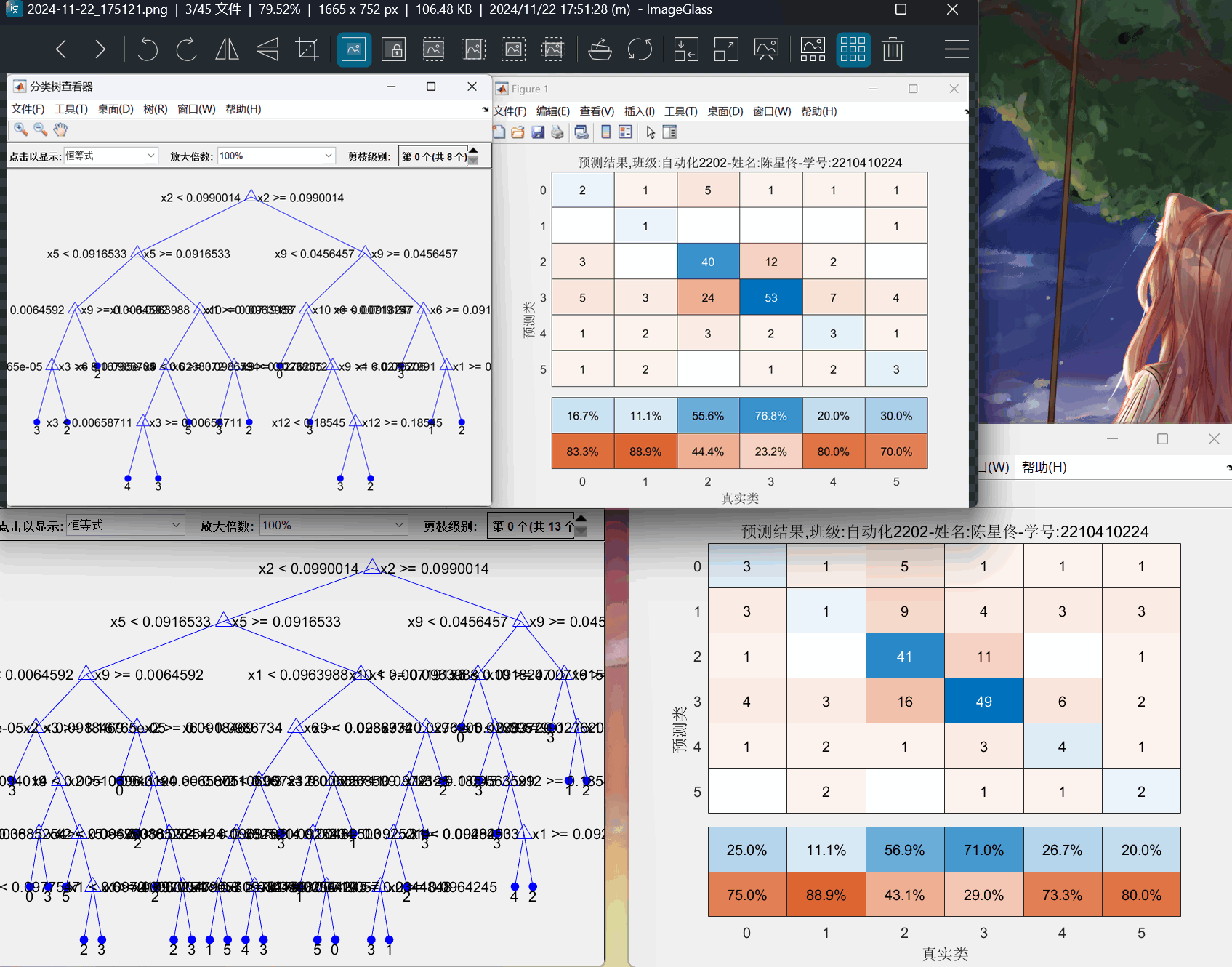
图5:决策树方案 分支=15、35的决策树结构图和混淆矩阵图
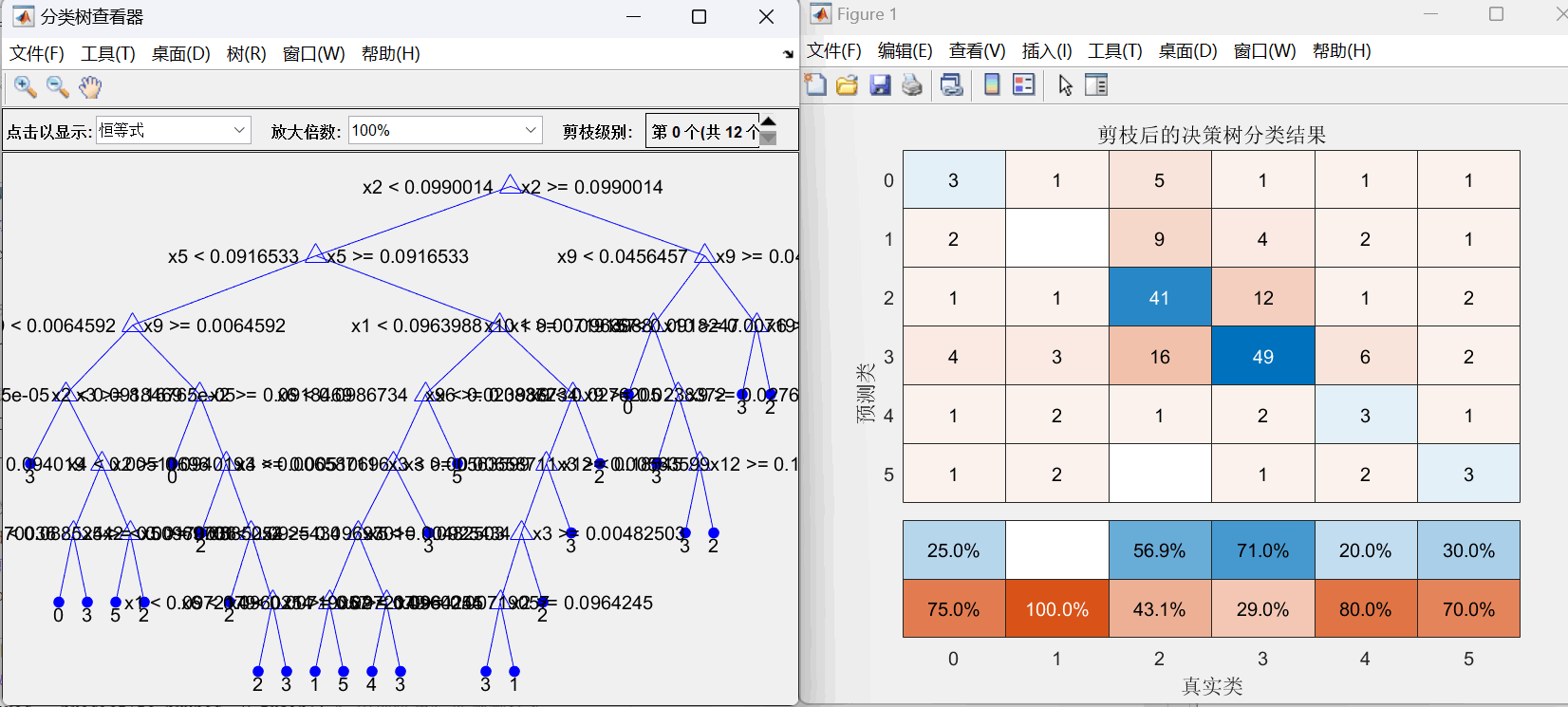
图6:决策树后剪枝方案 分支=35的决策树结构图和混淆矩阵图
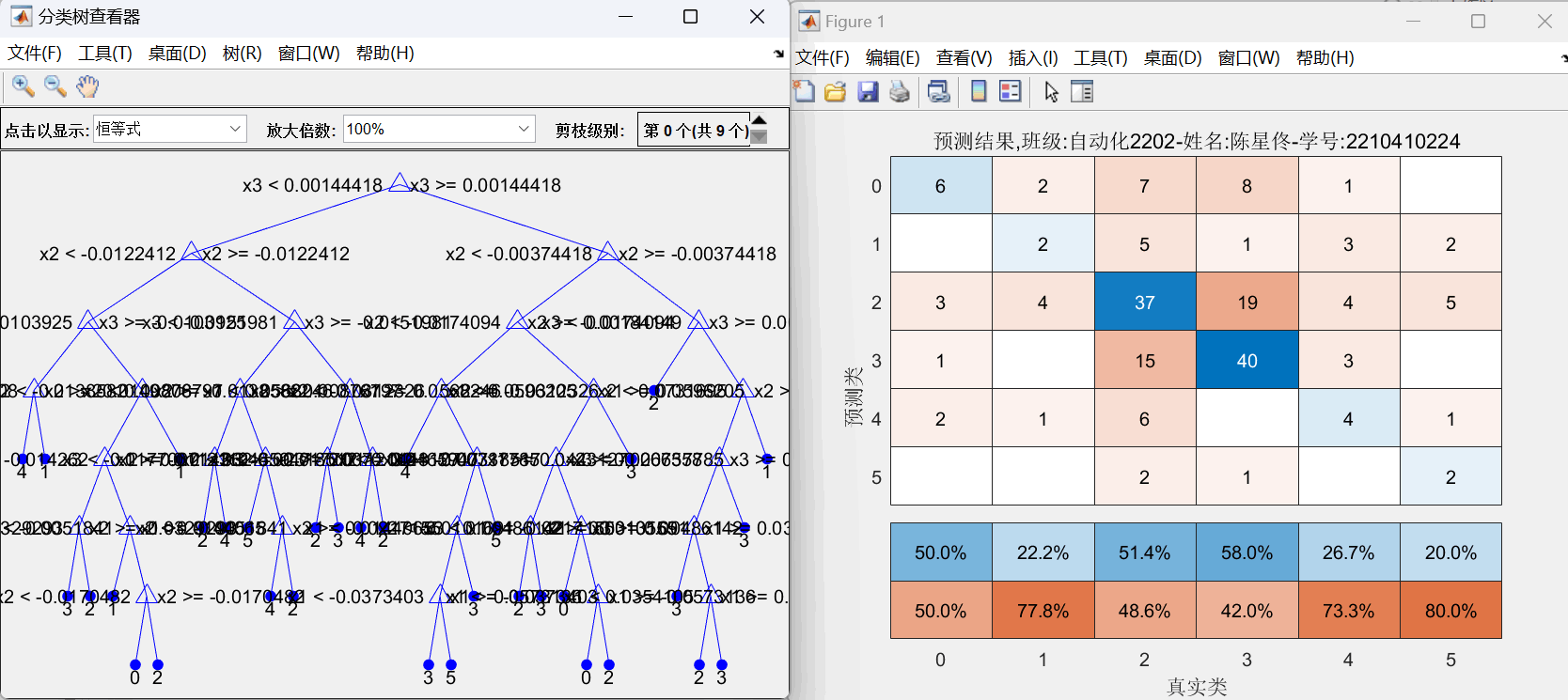
图7:决策树+PCA方案 分支=35的决策树结构图和混淆矩阵图
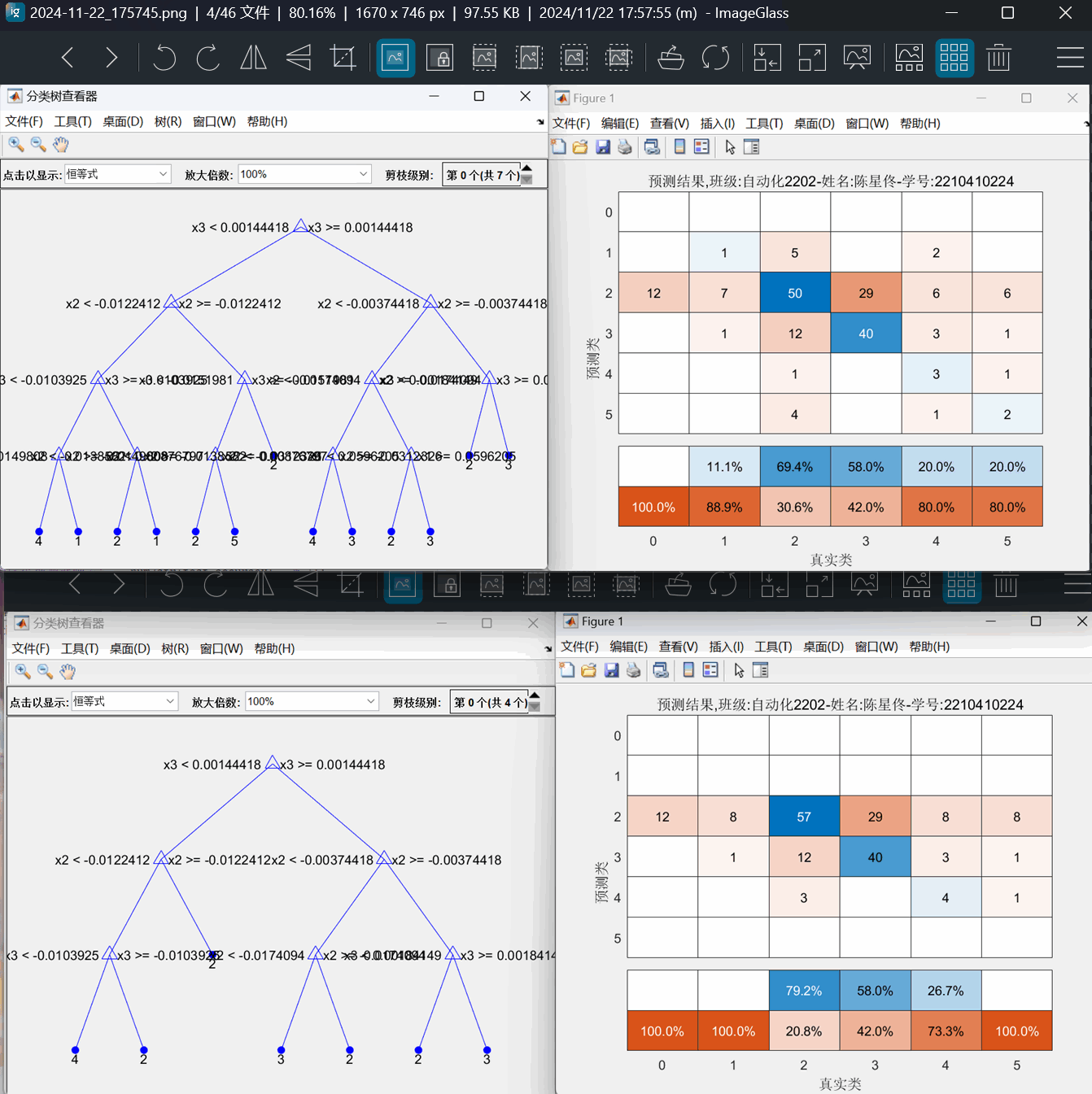
图8:决策树+PCA方案 分支=15、7的决策树结构图和混淆矩阵图
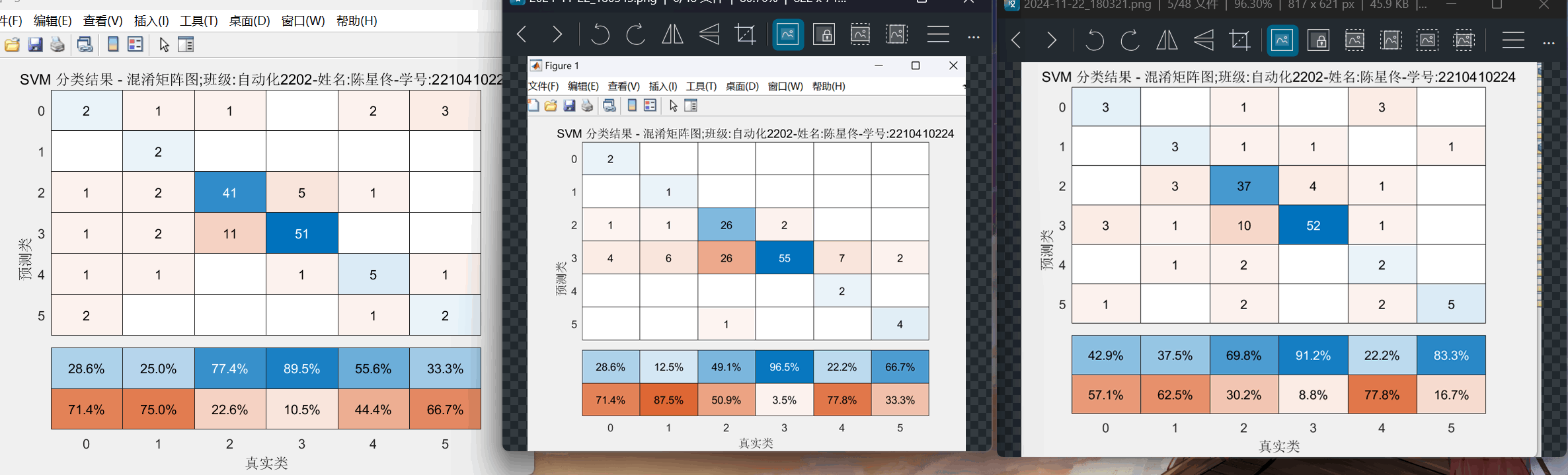
图9:SVM方案(线性核、高斯核、多项式核) 不使用数据归一化 混淆矩阵图
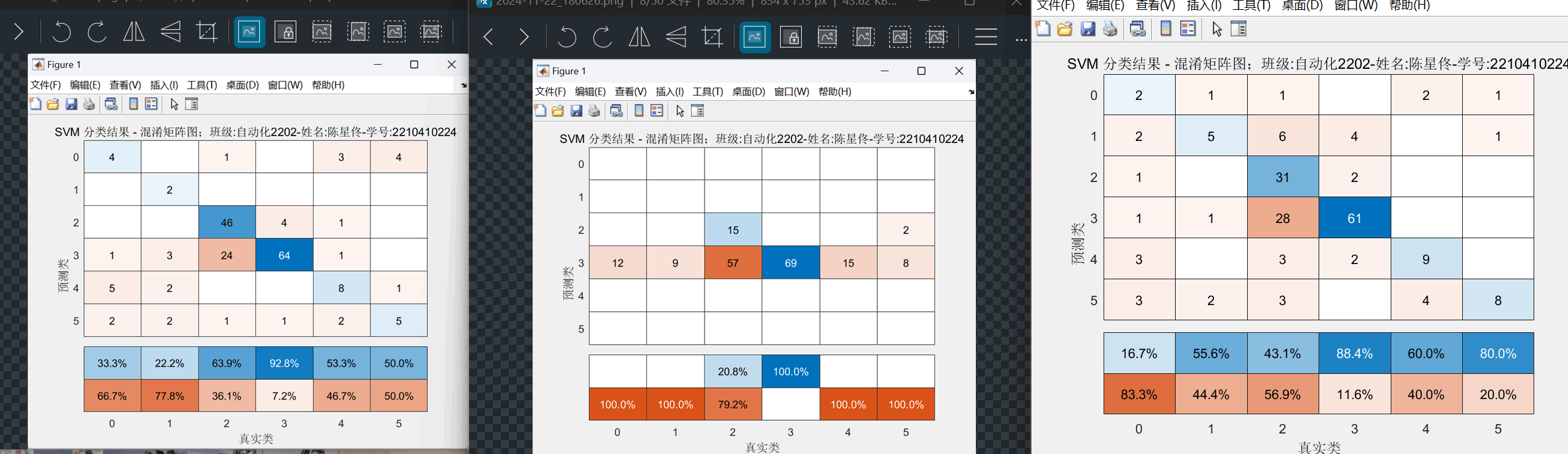
图10:SVM方案(线性核、高斯核、多项式核) 使用数据归一化 混淆矩阵图
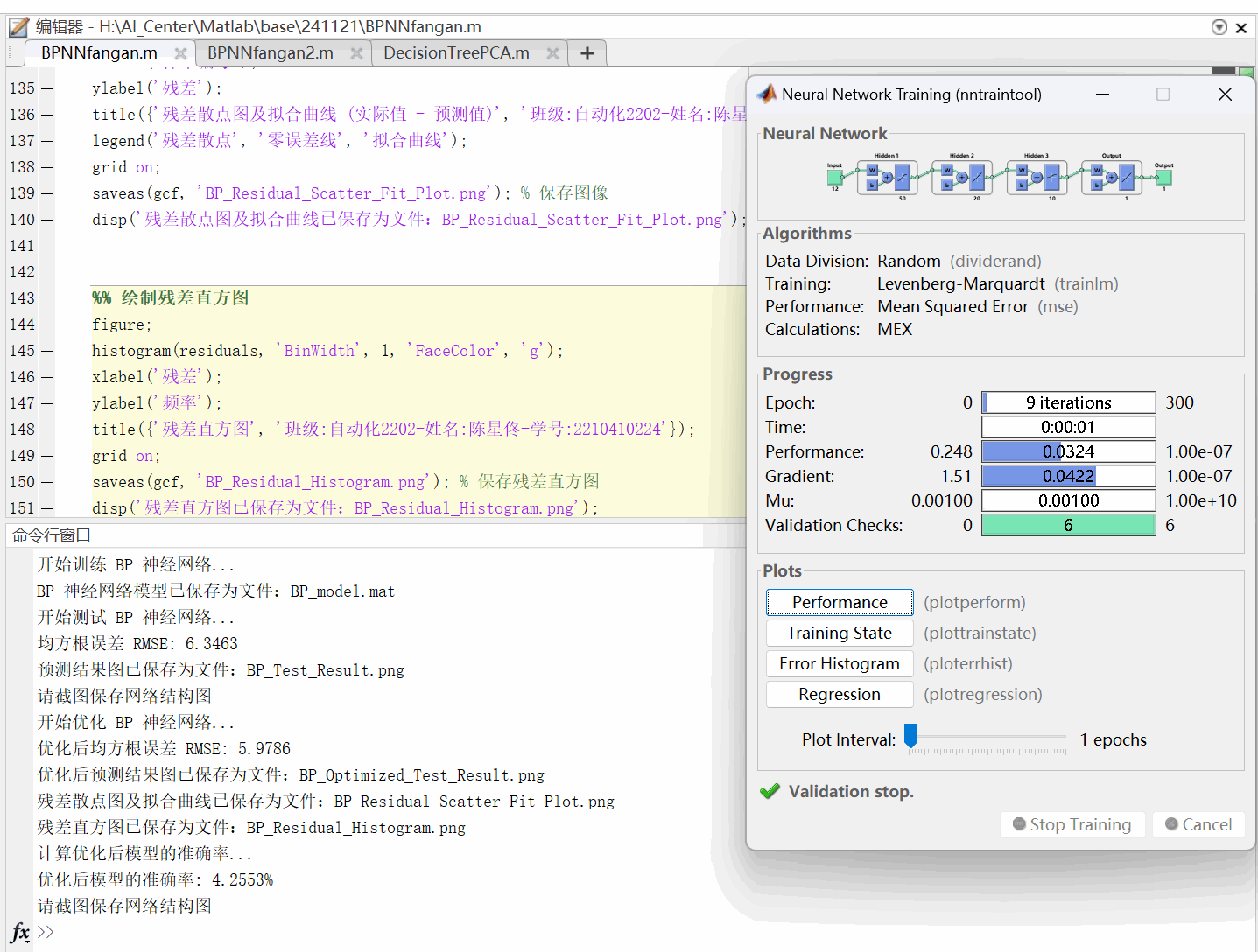
图11:BP神经网络训练参数图及模型准确率
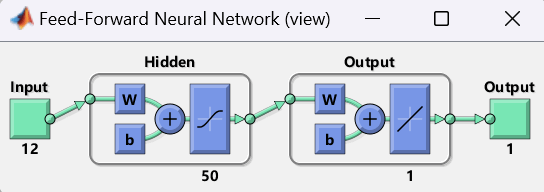
图12:单层BP神经网络结构图
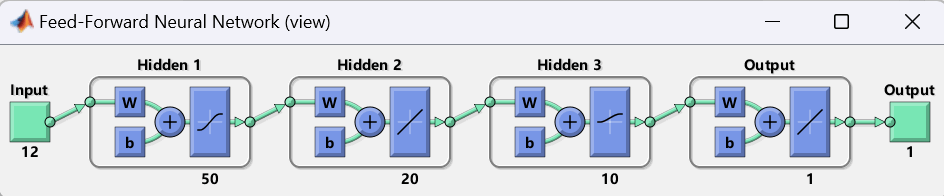
图13:多层BP神经网络结构图
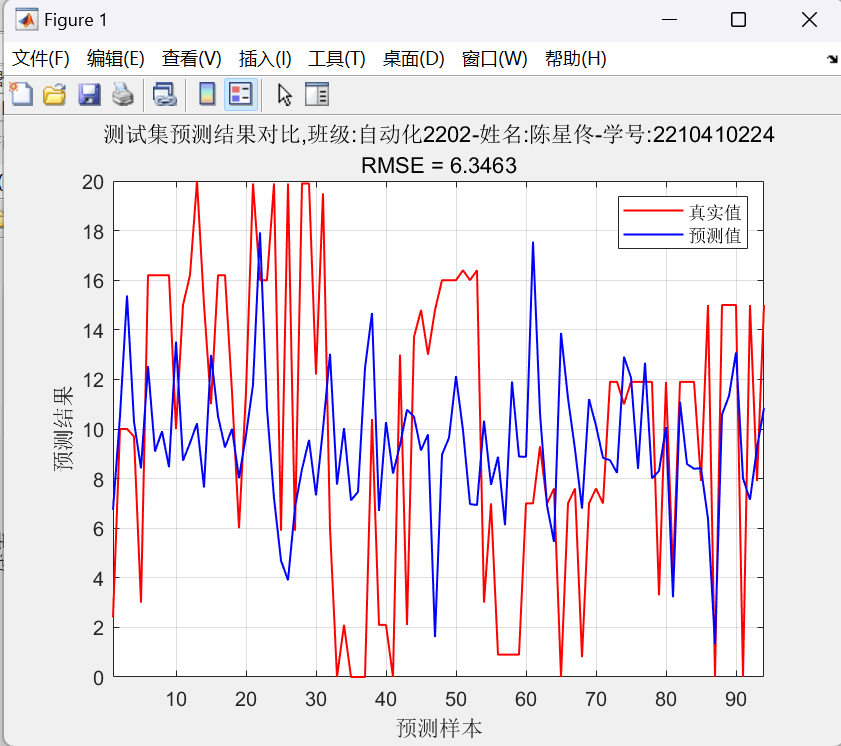
图14:单层BP神经网络预测结果对比图 均方根误差=6.3463<6.5
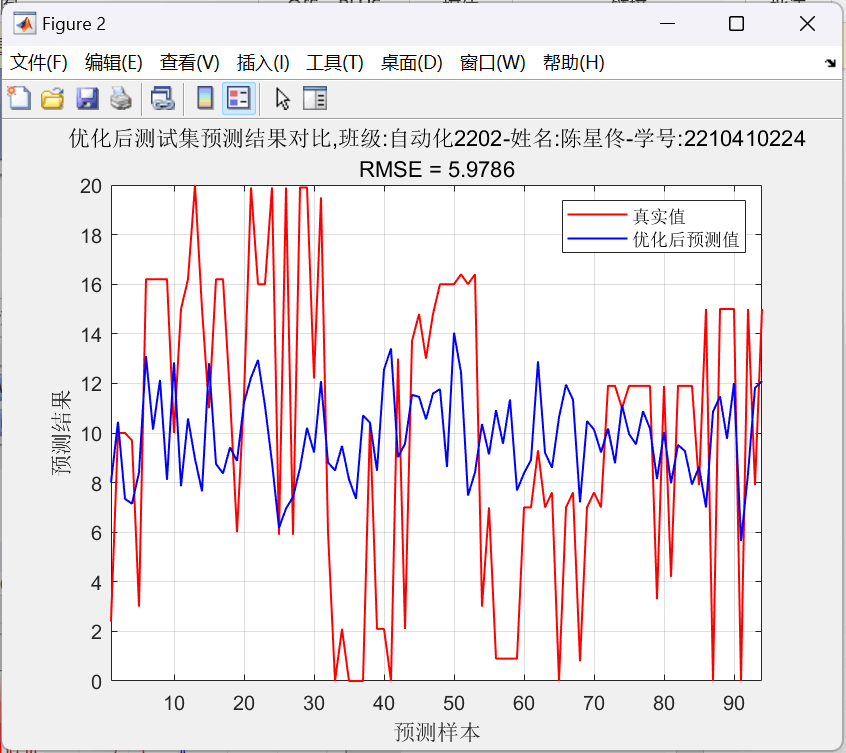
图15:多层BP神经网络预测结果对比图 均方根误差=5.9786<6.5
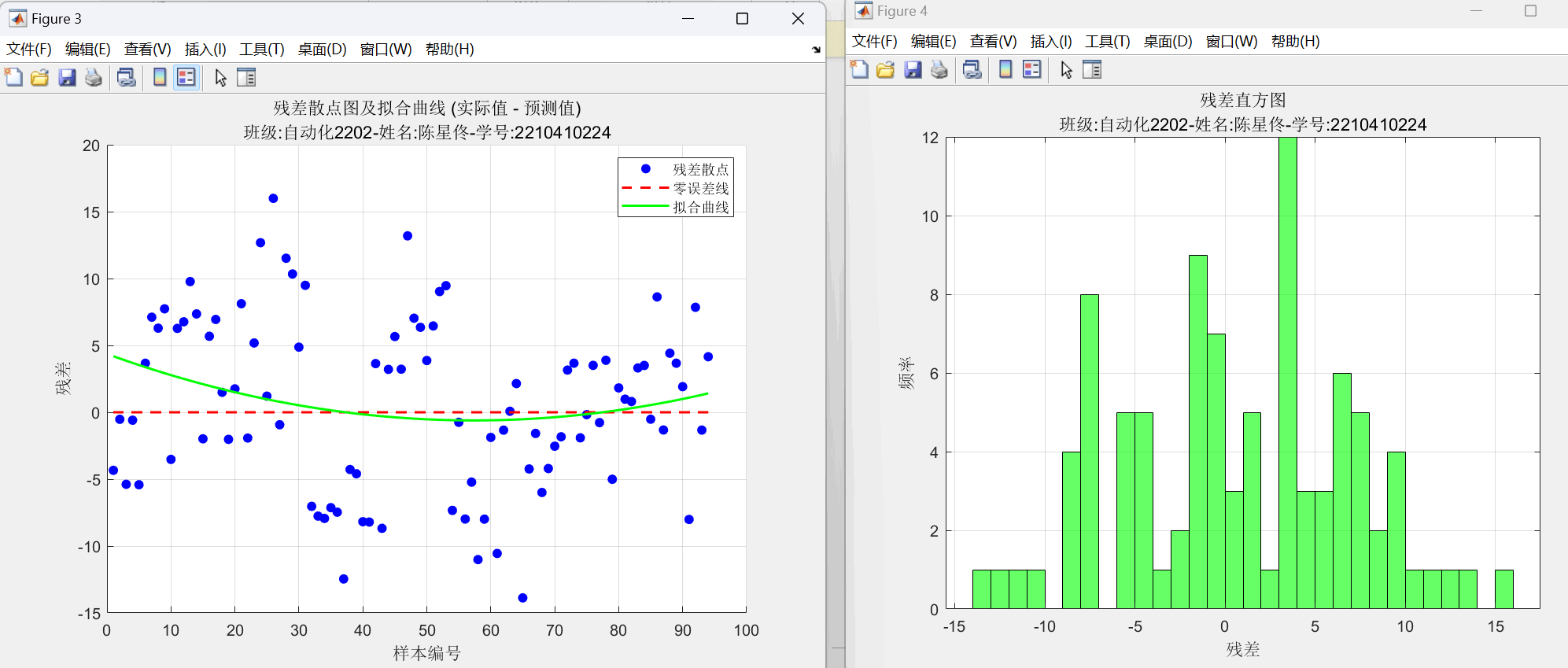
图16:最终BP神经网络输出残差散点图(含拟合曲线)和残差分布直方图
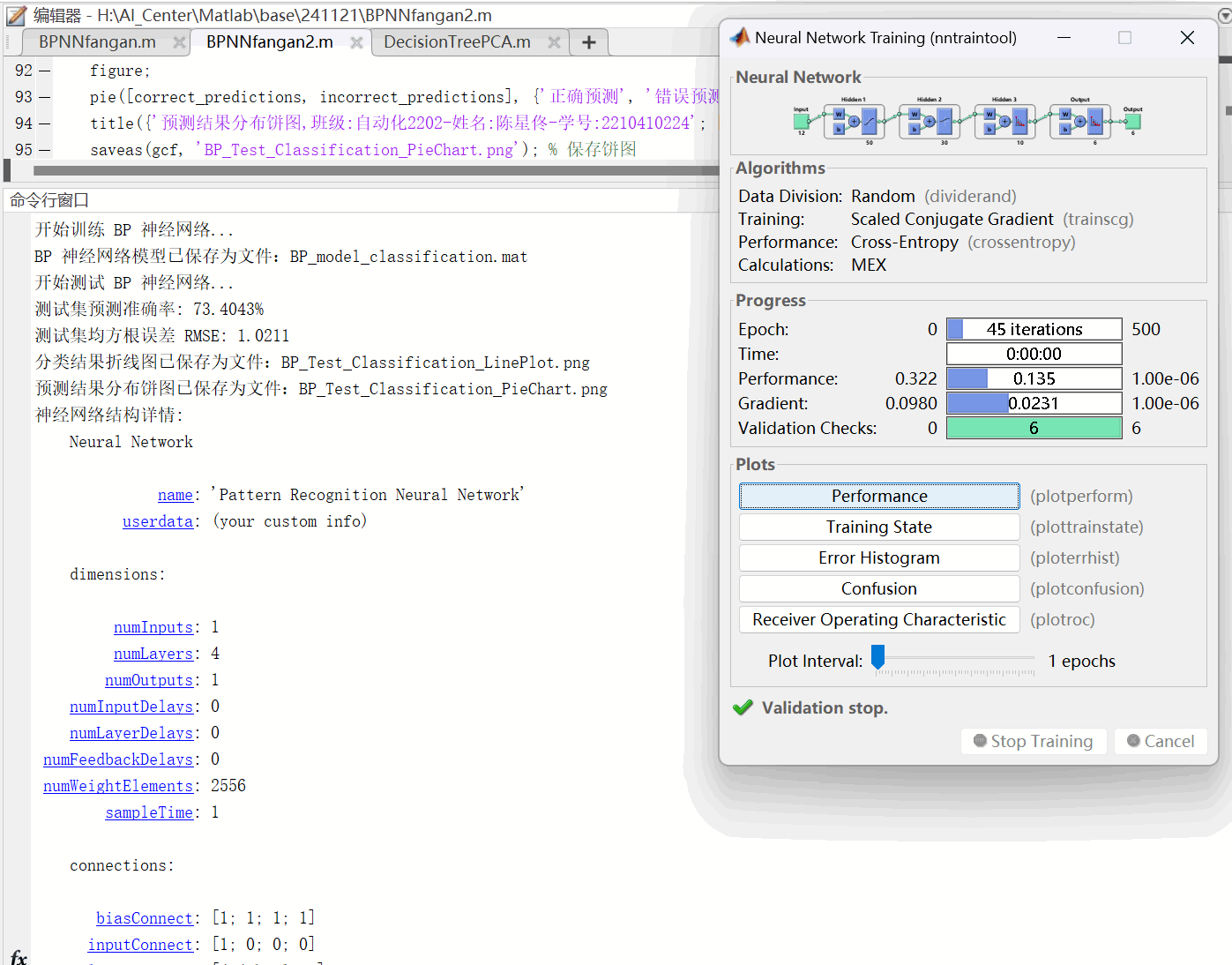
图17:重新设计的多层BP神经网络训练参数图及模型准确率
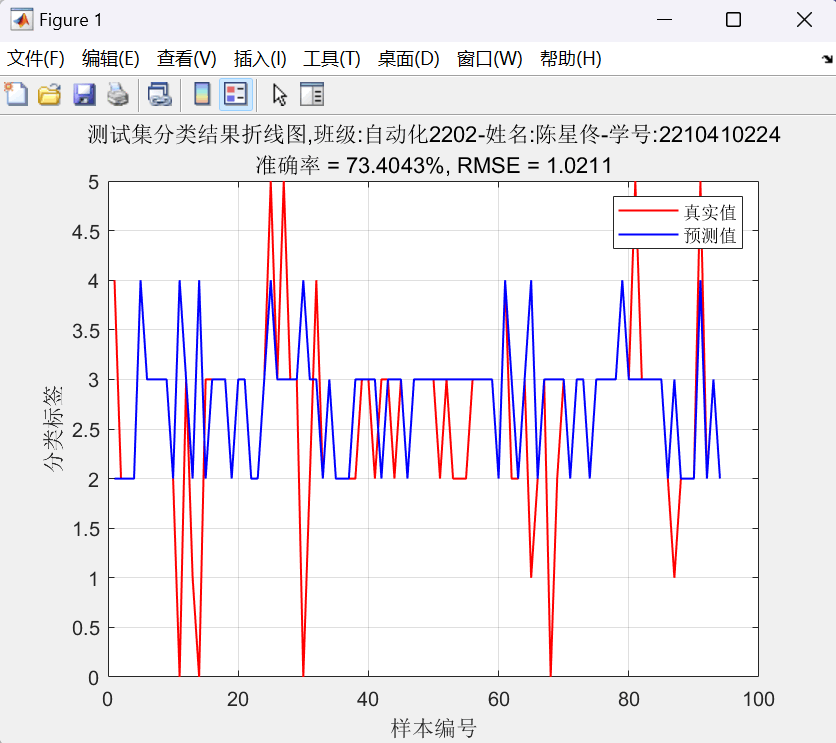
图18:重新设计的多层BP神经网络预测结果对比图(详细折线图) 均方根误差=1.0211<6.5
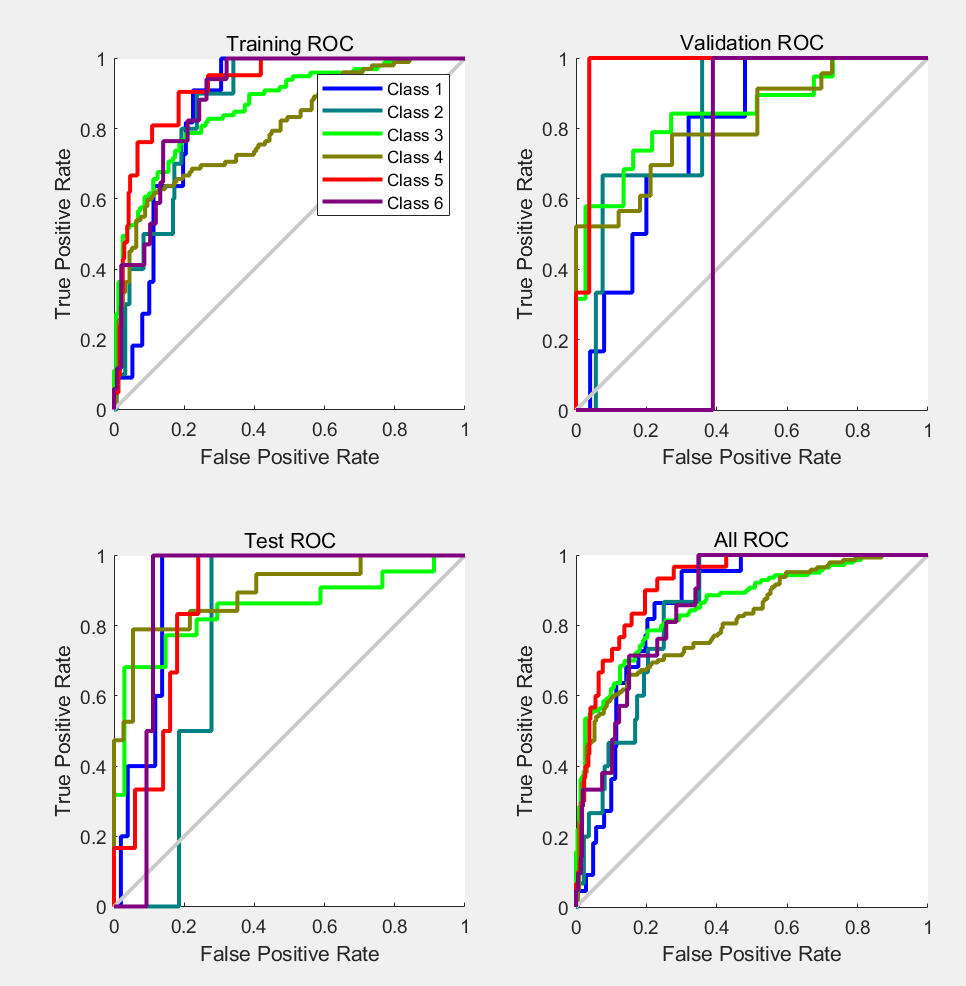
图19:重新设计的多层BP神经网络的评估指标:ROC曲线图
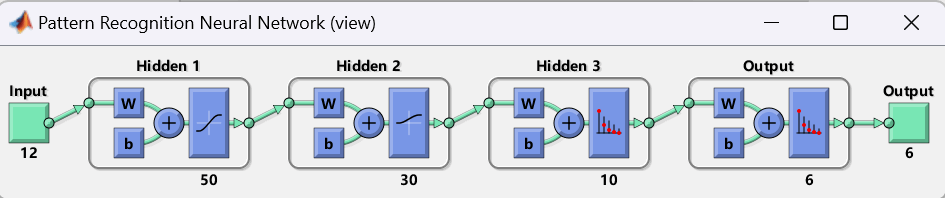
图20:重新设计的多层BP神经网络结构图
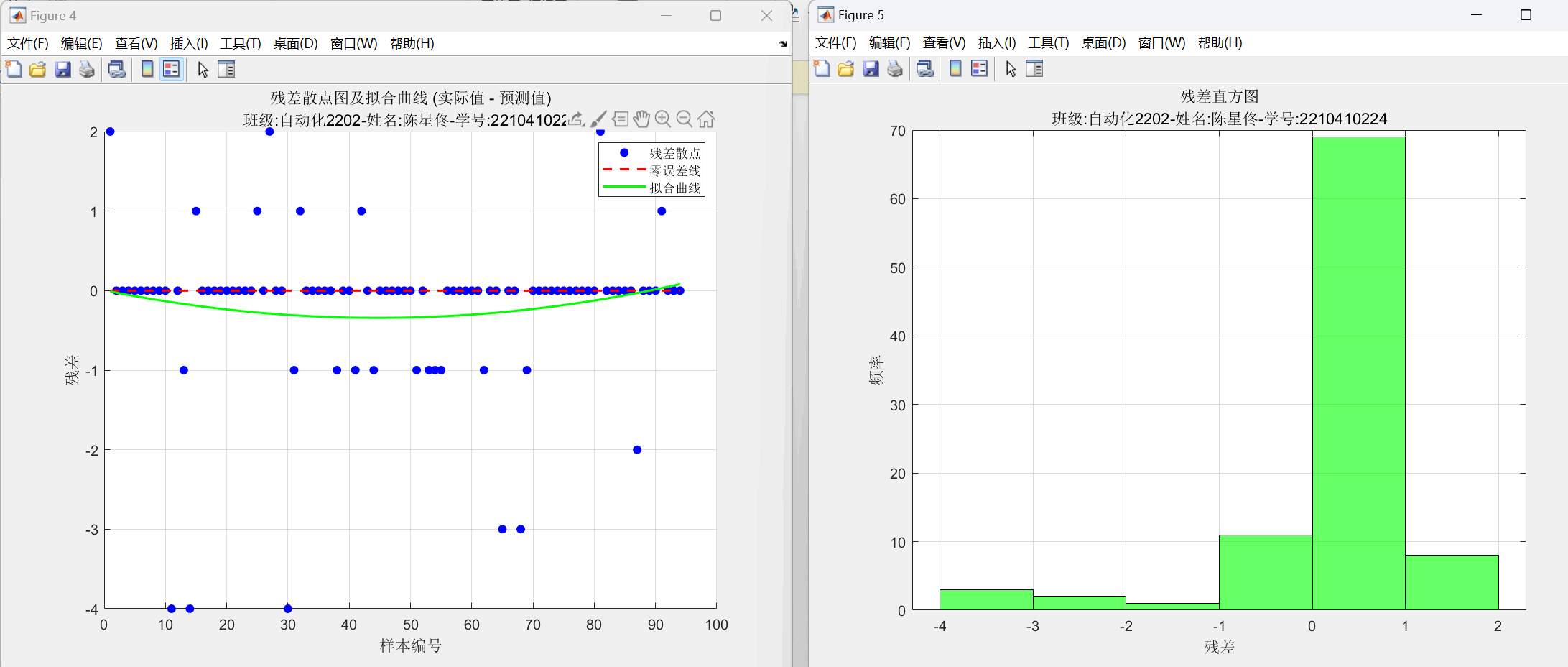
图21:重新设计的多层BP神经网络 残差散点图(含拟合曲线)和残差分布直方图
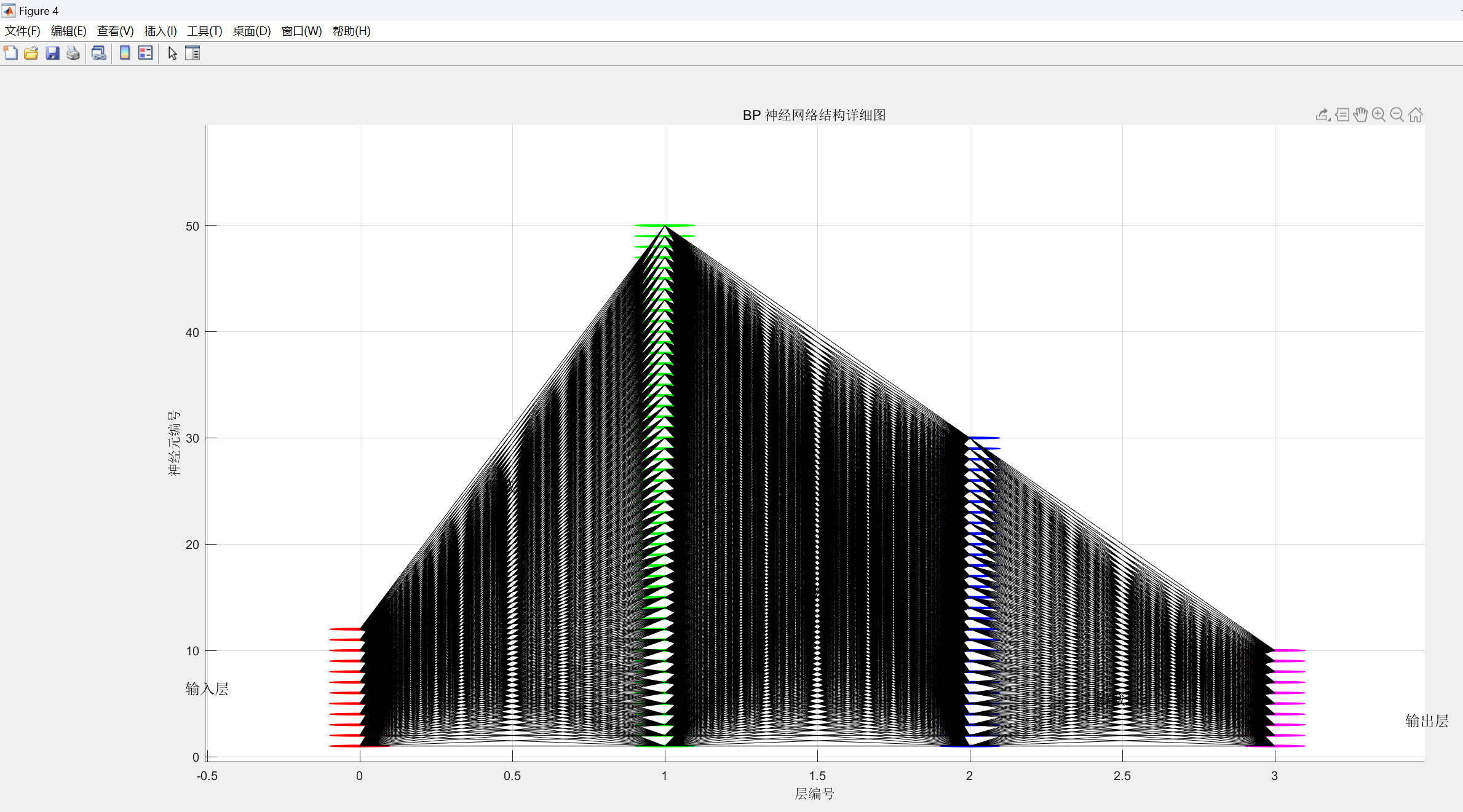
图22:重新设计的多层BP神经网络 内部结构图
图23:重新设计的多层BP神经网络 内部结构图
- 结果分析
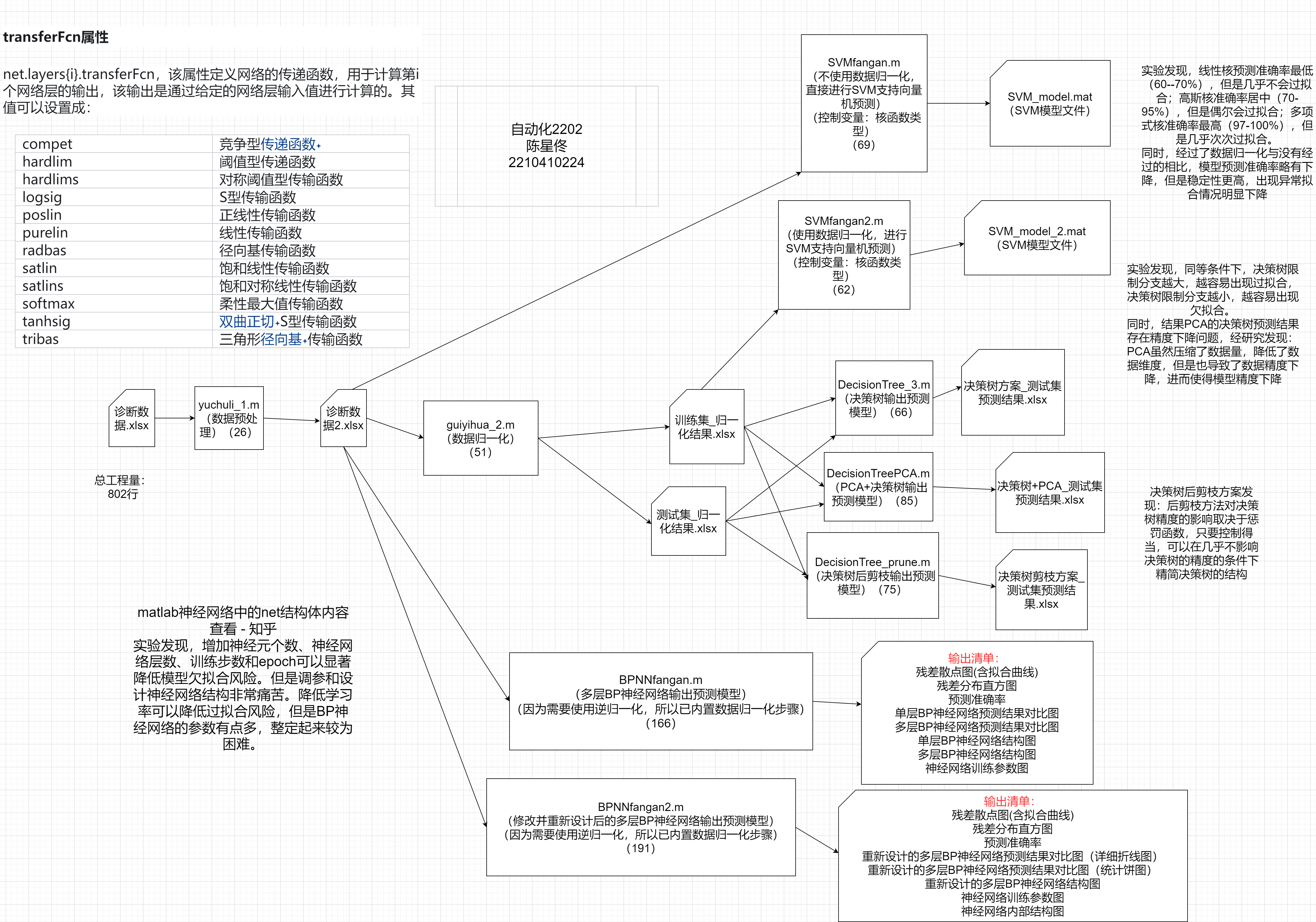
图24:项目结构图
经过参考资料发现,残差散点图和残差分布直方图可以更加直观地看出来模型的预测量和实际量的误差情况。前者可以看出细节部分,后者可以看出分布情况。
实验设计方案:
1 数据预处理:清洗数据、规范数据格式,保证样本的完整性和一致性。
需要记录:规范化之后的数据集
2 数据归一化:去除数据的单位限制,将其转化为无量纲的纯数值,便于不同单位或量级的指标能够进行比较和加权,加快训练网络的收敛性。
需要记录:归一化之后的数据集(训练集和测试集)
3 SVM模型方案:训练SVM模型,使用SVM进行预测,解决预测问题
需要记录:SVM模型文件、混淆矩阵图、模型准确率
4决策树方案:生成决策树模型,根据需要判断是否需要PCA或剪枝处理,并对模型进行评估。
需要记录:预测结果、决策树结构、模型准确率、混淆矩阵图
5 BP神经网络方案:先进行数据归一化,然后训练BP神经网络,最后对BP神经网络进行评估并绘制神经网络结构图。
需要记录:残差散点图、残差分布直方图、预测准确率、单层BP神经网络预测结果对比图、多层BP神经网络预测结果对比图、单层BP神经网络结构图、多层BP神经网络结构图、神经网络训练参数图。
**SVM模型调参思路:**从上到下,顺步进行。
第一步,选择核函数:
线性:尝试线性核。非线性:从 RBF 核开始。
第二步,优化调整关键参数:RBF 核:调优 C 和 γ。多项式核:调整degree 和 coef0。
第三步:结合交叉验证:确保参数对训练集和验证集均表现良好。
决策树调整思路:从简单到复杂,按顺序进行。
第一步:从简单模型开始:限制树深度,快速得到初步结果。
第二步:系统调整参数:重点优化max_depth、min_samples_split等核心参数。
第三步:结合验证集评估:通过交叉验证确保模型稳定性。
若是以上步骤均无法达标,则考虑集成学习。比如如果单棵树效果欠佳,可转为随机森林或梯度提升模型。
BP神经网络调参思路:先小后大,先部分后总体。
第一步:根据实验报告要求的均方根误差为第一指标,模型准确率和过拟合欠拟合状态为第二第三指标为基础进行调整。优先调整epoch、批尺寸、学习率和权值。
第二步:如果还是无法达标,就调整神经网络的神经元个数和激活函数的类型。
第三步:最后要是还是无法达标,就增加神经网络的层数。
好在最后不需要增加层数就能达到我的心理预期了,不然再加一层相当于前面的参数需要推倒重来一遍。
SVM模型方案的实验发现,线性核预测准确率最低(60--70%),但是几乎不会过拟合;高斯核准确率居中(70-95%),但是偶尔会过拟合;多项式核准确率最高(97-100%),但是几乎次次过拟合。
同时,经过了数据归一化与没有经过的相比,模型预测准确率略有下降,但是稳定性更高,出现异常拟合情况明显下降
决策树方案实验发现,同等条件下,决策树限制分支越大,越容易出现过拟合,决策树限制分支越小,越容易出现欠拟合。
同时,结果PCA的决策树预测结果存在精度下降问题,经研究发现:PCA虽然压缩了数据量,降低了数据维度,但是也导致了数据精度下降,进而使得模型精度下降。
决策树后剪枝方案发现:后剪枝方法对决策树精度的影响取决于惩罚函数,只要控制得当,可以在几乎不影响决策树的精度的条件下精简决策树的结构。
BP神经网络方案实验发现,增加神经元个数、神经网络层数、训练步数和epoch可以显著降低模型欠拟合风险。但是调参和设计神经网络结构非常痛苦。降低学习率可以降低过拟合风险,但是BP神经网络的参数有点多,整定起来较为困难。
作业4-1归一化对实验结果的影响
归一化的作用:
归一化是将数据特征值缩放到相同的范围(如 [0,1] 或 [-1,1]),在决策树算法中:
决策树基于特征的分裂点来划分数据,因此归一化对决策树模型的性能没有直接影响,因为决策树对特征的尺度不敏感。
归一化可能间接影响实验结果:如果数据包含大范围的特征值,归一化有助于在多模型实验中提高模型的统一性。
实验观察发现:通过对归一化和非归一化数据分别进行训练和测试,通常决策树模型的分类结果差异较小,尤其是数据分布良好时。但是,当数据分布极为不均衡或特征尺度差异较大时,归一化能提升训练的稳定性。
作业4-2决策树的过拟合特性
决策树模型倾向于最大化训练数据的分类准确率,这可能导致树的深度过深、分支过多,进而对训练集的噪声和偶然性模式过度拟合。
过深的决策树会导致在测试集上性能下降,即模型复杂度过高、泛化能力差。
其表现特征为:
训练集准确率接近 100%,但测试集准确率显著下降。
混淆矩阵中某些类别预测效果极好,但其他类别的错误率很高。
作业4-3抑制决策树过拟合的方法
限制树的最大深度(MaxDepth):设置决策树的最大深度,限制树的分裂次数。
设置最小分裂样本数(MinLeafSize):要求每个叶节点包含的最少样本数量,防止小样本数据被过度拟合。
后剪枝(Post-Pruning):使用训练后的决策树,通过交叉验证找到最优子树,将不必要的分支剪除。
交叉验证:使用交叉验证评估树的性能,选择最优分裂点或剪枝深度。